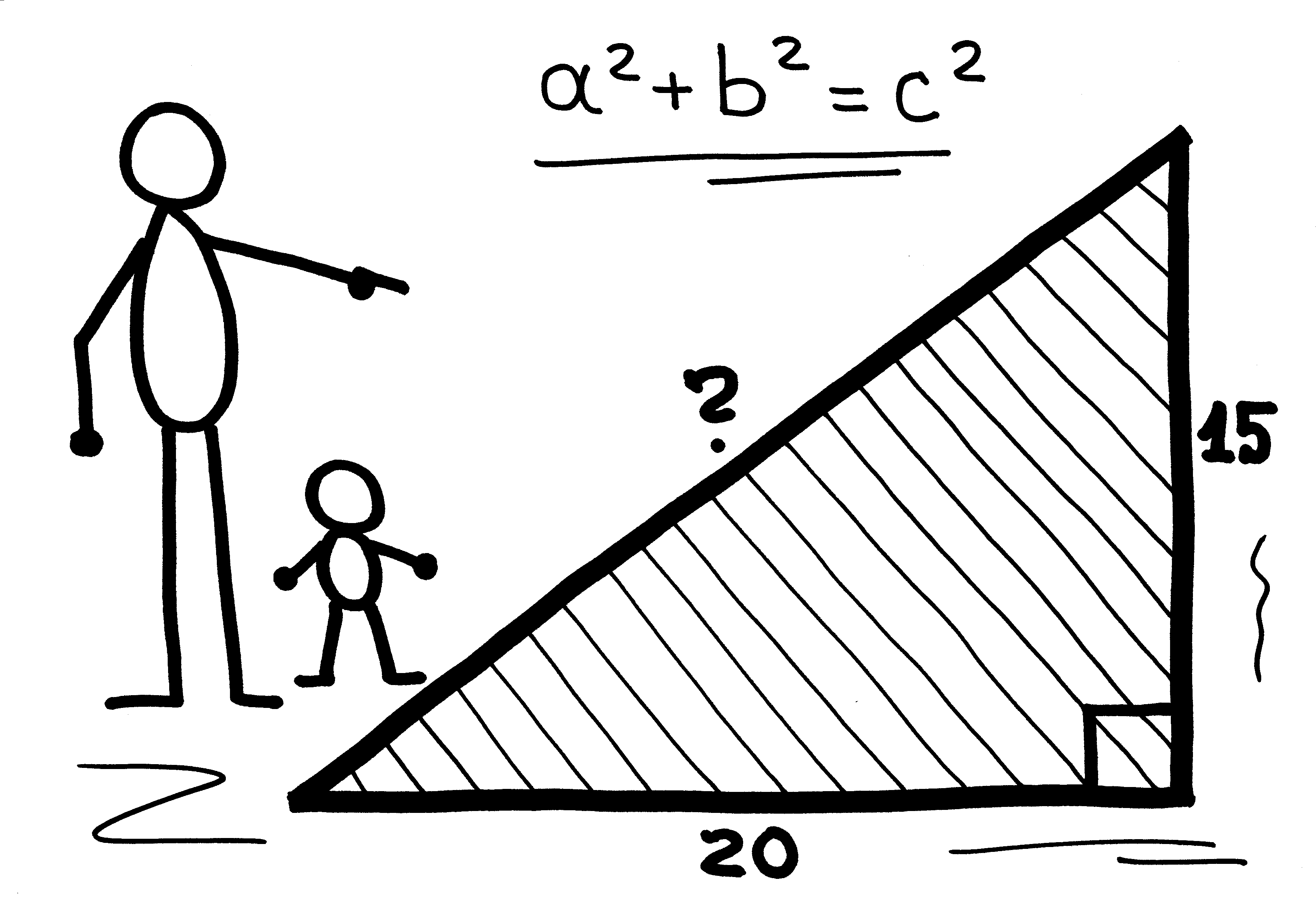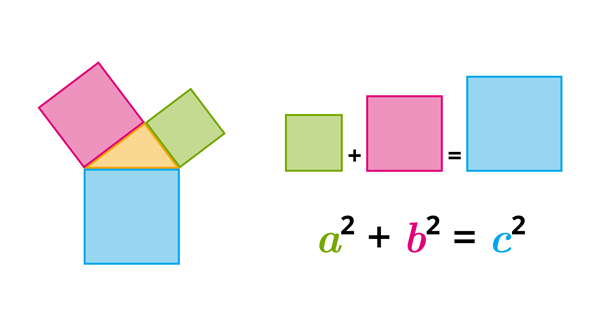Теорема Пифагора - одна из самых известных математических теорем, которая устанавливает связь между сторонами прямоугольного треугольника. Исторически она связана с именем древнегреческого математика Пифагора, который жил примерно в 570-490 годах до н.э. В настоящей статье мы рассмотрим основные аспекты теоремы Пифагора, ее формулу, доказательство и применение в задачах.
Cодержание
Введение
Теорема Пифагора - одна из самых известных математических теорем, которая устанавливает связь между сторонами прямоугольного треугольника. Исторически она связана с именем древнегреческого математика Пифагора, который жил примерно в 570-490 годах до н.э. Пифагор был не только математиком, но и мыслителем и философом, а его философия и образ жизни привлекли многих последователей. В настоящей статье мы рассмотрим основные аспекты теоремы Пифагора, ее формулу, доказательство и применение в задачах.

Основные факты о Пифагоре
Биографические факты о жизни Пифагора не дошли до нас, и все, что мы знаем о нем, основано на произведениях других древнегреческих философов. Известно, что Пифагор общался с известными мудрецами и учеными своего времени, и пробыл долгое время в Египте, изучая местные таинства. Он достиг больших успехов в математике и ему приписывают открытие и доказательство теоремы Пифагора, а также создание таблицы Пифагора.

Что такое теорема Пифагора?
Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Важно отметить, что в прямоугольном треугольнике гипотенуза больше любого из катетов, и сторону прямоугольного треугольника, противолежащую прямому углу, называют гипотенузой, а стороны, прилежащие к прямому углу, - катетами.
См. также
Формула теоремы Пифагора
Формула теоремы Пифагора имеет следующий вид:
| c² | = | a² + b² |
|---|
Отсюда можно вывести следующие выражения:
- a = √(c² - b²)
- b = √(c² - a²)
- c = √(a² + b²)

Доказательство теоремы Пифагора
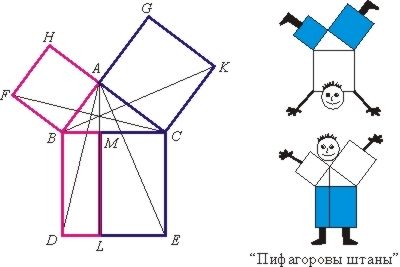
Существует множество доказательств теоремы Пифагора различными математическими методами. Одно из самых наглядных связано с площадями. Рассмотрим несколько доказательств:
Первое доказательство:
Построим квадрат, сторона которого равна сумме катетов данного треугольника a + b. Площадь квадрата равна (a + b)². Теперь проведем гипотенузы c, которые образуют квадрат внутри построенного квадрата. Стороны четырехугольника равны c, а углы - прямые. Следовательно, площадь квадрата состоит из четырех площадей равных прямоугольным треугольникам и площади квадрата, образованного гипотенузами.
Второе доказательство:
На двух сторонах квадрата поменяем местами отрезки a и b, при этом длина стороны квадрата не меняется. Теперь площадь квадрата можно сложить из двух площадей квадратов, образованных катетами a и b, и двух площадей прямоугольников.
Третье доказательство:
Используя алгебраические преобразования, можно доказать теорему Пифагора следующим образом: c² + 4ab² = (a + b)²; c² + 2ab = a² + 2ab + b²; c² = a² + b².
Применение теоремы Пифагора в задачах
Теорема Пифагора актуальна в заданиях как базового, так и профильного ЕГЭ по математике. За верное решение задач базового уровня дается 1 балл, за задания повышенного уровня начисляется 3 балла. Применение теоремы Пифагора в задачах помогает определить, является ли треугольник прямоугольным и находить значения его сторон.
См. также
Заключение
Теорема Пифагора является одной из основных и наиболее известных теорем в математике. Ее формула и доказательство дают возможность решать различные задачи, связанные с прямоугольными треугольниками. Знание и применение этой теоремы является основой для понимания геометрии и алгебры.