Гипербола и парабола являются важными объектами изучения в математике. Гипербола - геометрическое место точек, для которых абсолютное значение разности расстояний до фокусов постоянно. Парабола - кривая второго порядка с уравнением у=ax^2+bx+c. Узнайте больше о свойствах и форме гиперболы и параболы. - NOCFN
Cодержание
Гипербола (др.-греч. ὑπερβολή, от ὑπερ - "верх" + βαλειν - "бросать") - геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно. Гипербола является коническим сечением и квадрикой, наряду с эллипсом и параболой. Гипербола может быть определена несколькими путями.
Коническое сечение
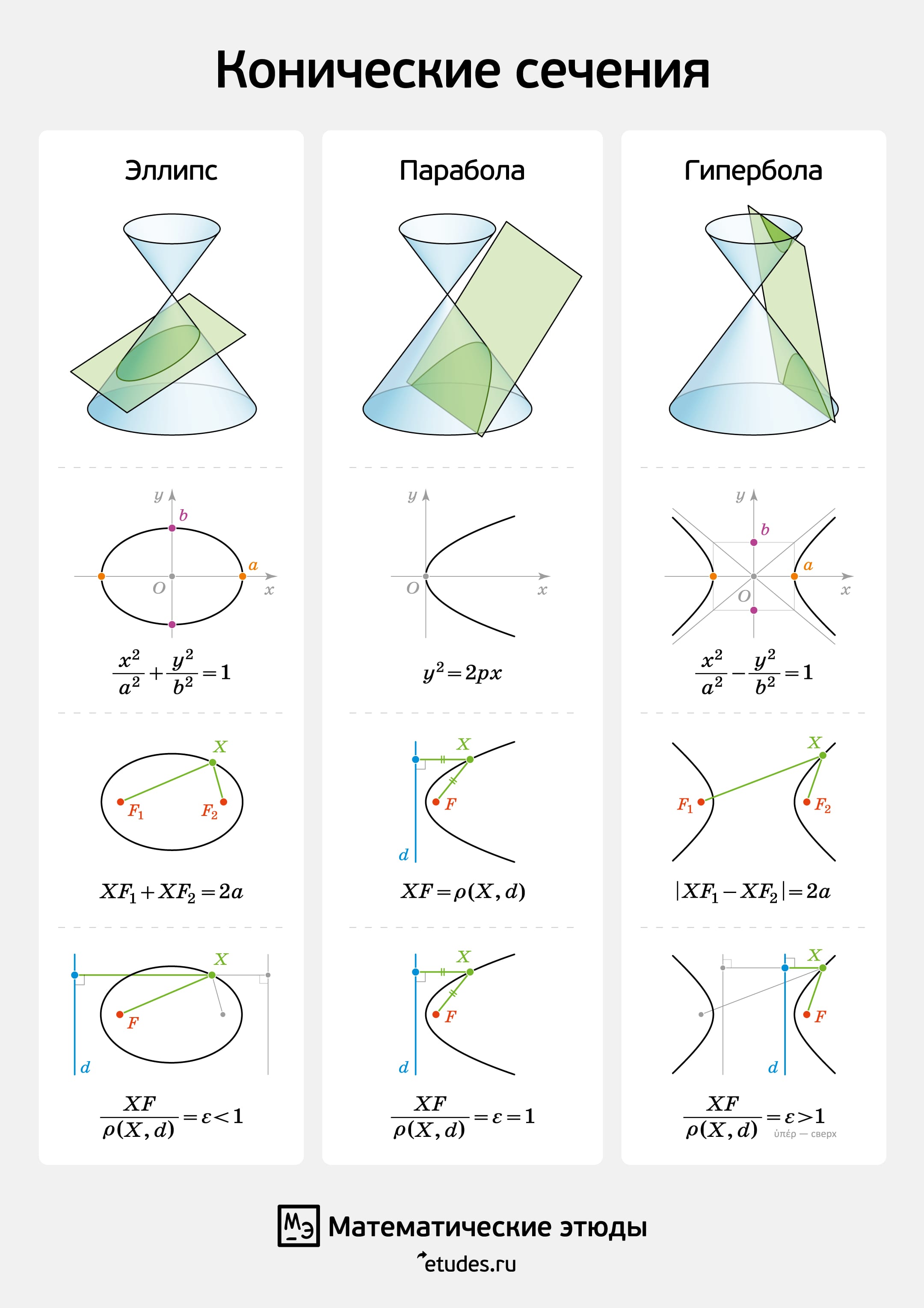
Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. При таком определении, гипербола является одним из результатов сечения конуса плоскостью, вместе с параболой, эллипсом и другими вырожденными случаями. Например, пересекающиеся и совпадающие прямые, а также точка, возникают, когда секущая плоскость проходит через вершину конуса. Если пересекающиеся прямые считать вырожденной гиперболой, она будет совпадать со своими асимптотами.
Как геометрическое место точек
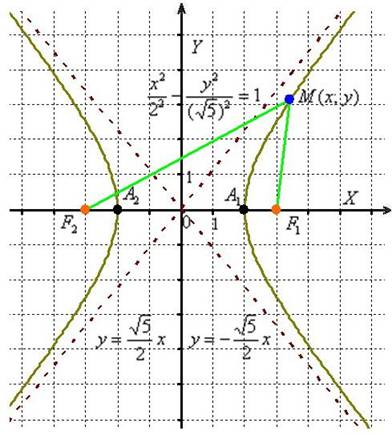
Гипербола также может быть определена как геометрическое место точек, для которых абсолютное значение разности расстояний от точки до двух заданных точек, фокусов, является постоянным. Это определение позволяет лучше понять свойства и форму гиперболы. Разность расстояний от точек гиперболы до фокусов всегда будет одинаковой.
Через директрису и фокус
Третий способ определения гиперболы - через отношение расстояния до фокуса и до заданной прямой, называемой директрисой. Гипербола - это геометрическое место точек, для которых отношение расстояния до фокуса и до директрисы постоянно и больше единицы. Заданная постоянная, называемая эксцентриситетом (ε), определяет форму гиперболы. Если ε > 1, то гипербола будет открытой и иметь две ветви, которые приближаются к асимптотам.

Гипербола и парабола в математике
Гипербола и парабола являются важными объектами изучения в математике и имеют свои уникальные свойства и особенности.
Гипербола
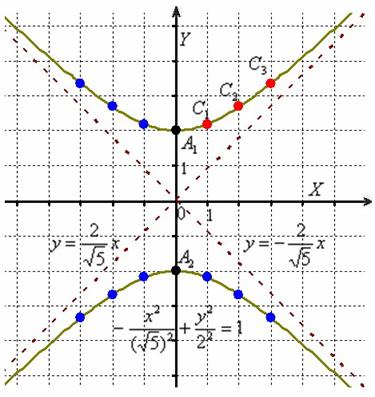
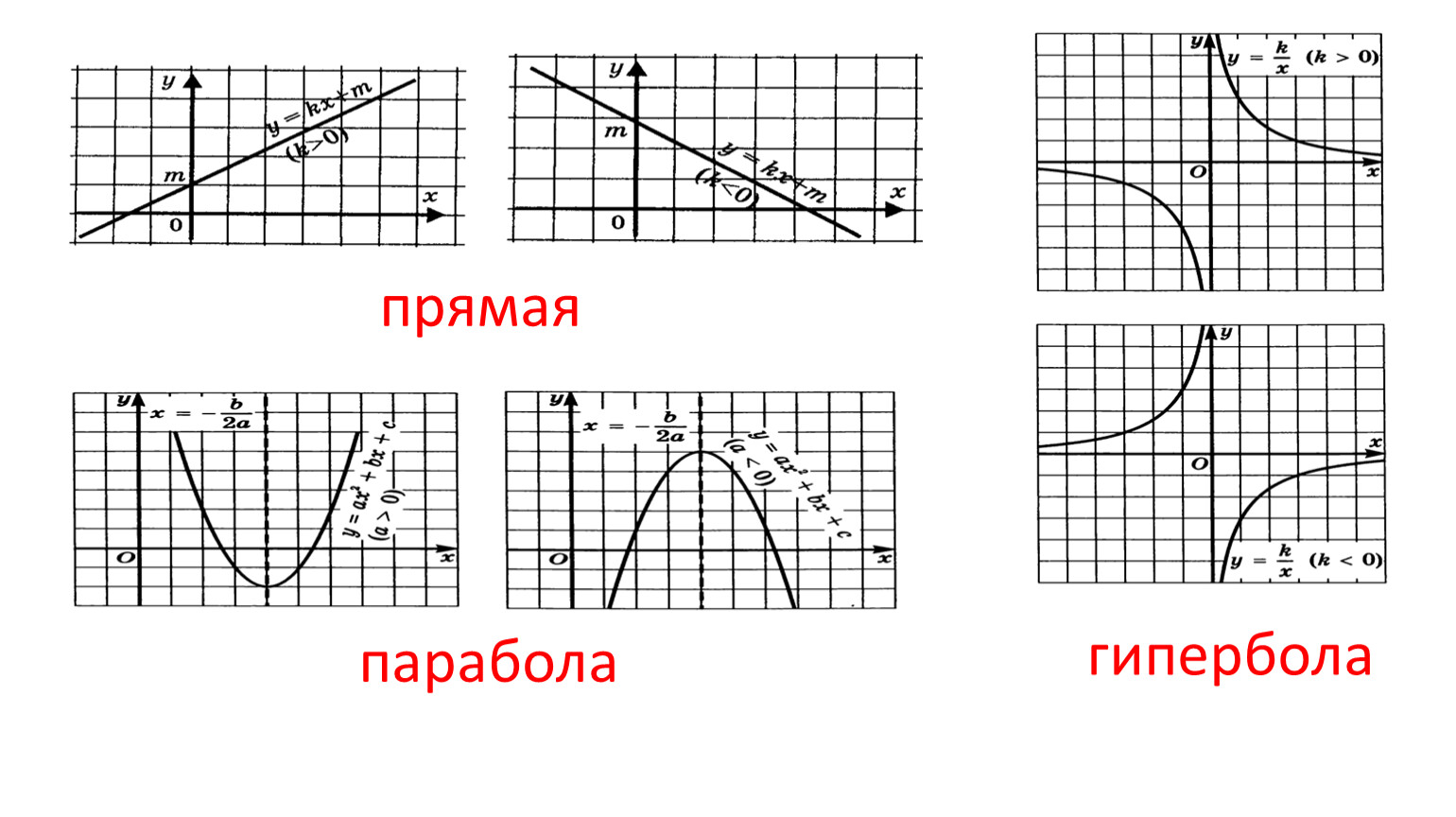
Гипербола может быть представлена уравнением вида у=k/x, где k - постоянное значение. Если гипербола имеет равные ветви, она называется равнобочной гиперболой. Гипербола имеет две ветви, которые приближаются к асимптотам. Фокусы гиперболы (F1 и F2) являются двумя фиксированными точками, а межфокусное расстояние (2с) - расстоянием между фокусами.
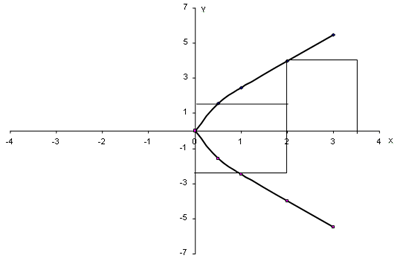
Парабола
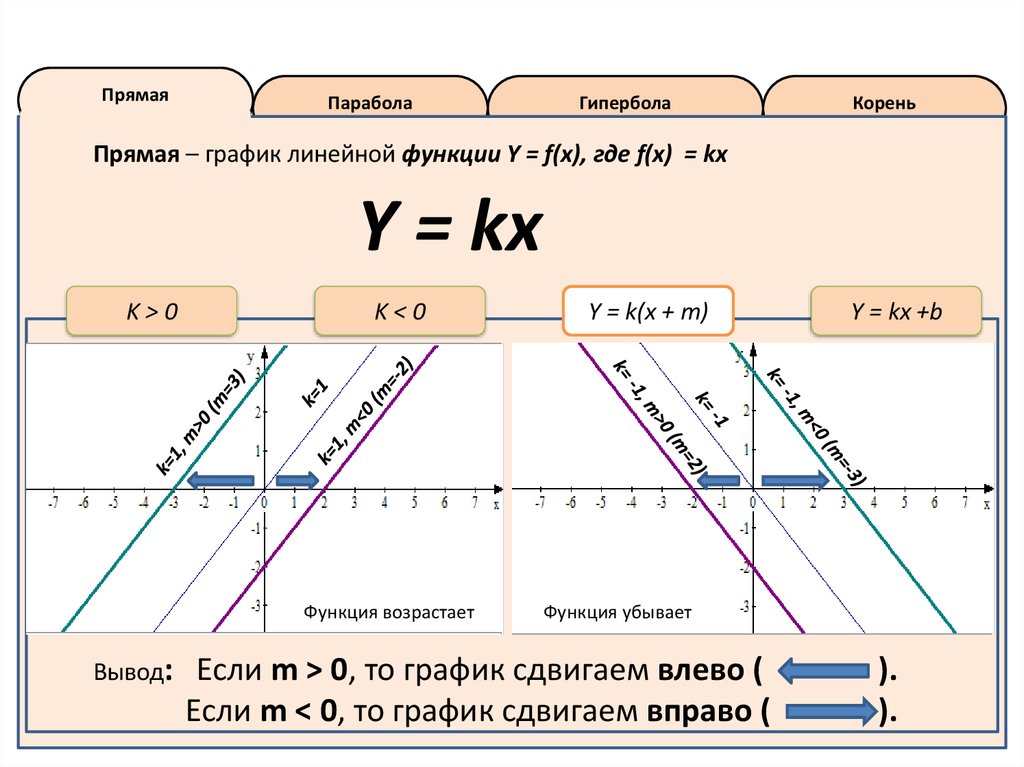
Парабола также является кривой второго порядка, но отличается от гиперболы своей формой и свойствами. Парабола может быть представлена уравнением вида у=ax^2+bx+c, где a, b и c - коэффициенты. Парабола имеет одну ветвь и симметрична относительно своей вершины. Вершина параболы является экстремумом функции, которая описывает параболу.

Заключение
Гипербола и парабола - это две важные кривые в математике, которые имеют свои уникальные свойства и определения. Гипербола представляет собой геометрическое место точек, для которых абсолютное значение разности расстояний до фокусов постоянно. Парабола же является кривой второго порядка, которая может быть представлена уравнением вида у=ax^2+bx+c. Обе кривые имеют широкое применение в различных областях математики и науки.
См. также
Что нам скажет Википедия?
Гипербола (др.-греч. ὑπερβολή, от ὑπερ - "верх" + βαλειν - "бросать") - геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно.
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, бо́льшим единицы.
Гипербола может быть определена несколькими путями.
Коническое сечение: Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
Как геометрическое место точек: Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Через директрису и фокус: Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная ε > 1 называется эксцентриситетом гиперболы.