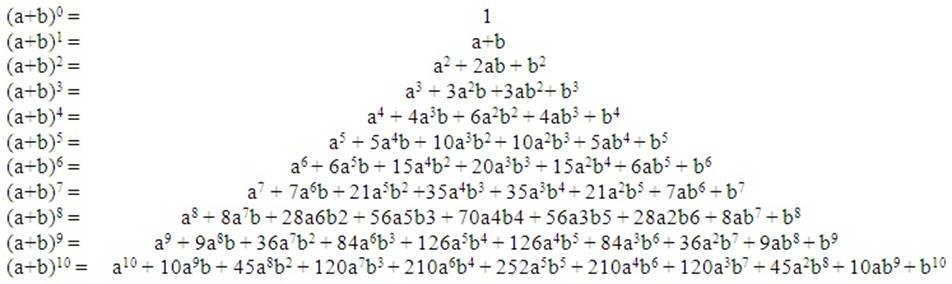Узнайте, как вычисляется треугольник Паскаля, бесконечная таблица биномиальных коэффициентов. Изучите свойства и особенности этого математического инструмента.
Cодержание
История
Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). В Италии треугольник Паскаля иногда называют «треугольником Тартальи», поскольку Никколо Тарталья описал эту таблицу на сто лет раньше Паскаля. На титульном листе учебника арифметики, написанного в 1529 году Петером Апианом, астрономом из Ингольштадтского университета, также изображён треугольник Паскаля. А в 1665 году вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике», которая была специально посвящена данной таблице и по содержательности опережала своих предшественников.

Обозначения и свойства
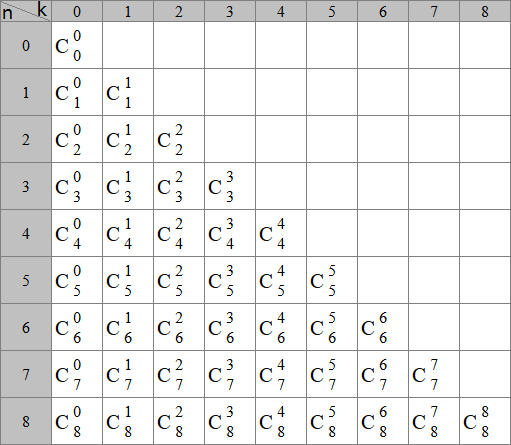
Биномиальные коэффициенты часто обозначаются или и читаются как «число сочетаний из n элементов по k».
Цитаты
См. также
См. также
Примечания

Литература
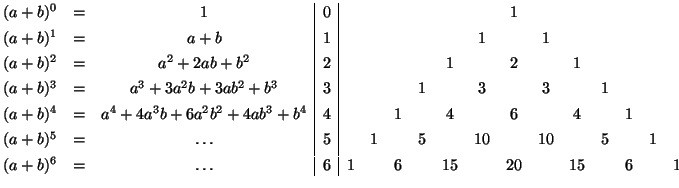
Ссылки
Числовой треугольник Паскаля — неисчерпаемый источник всевозможных математических радостей.
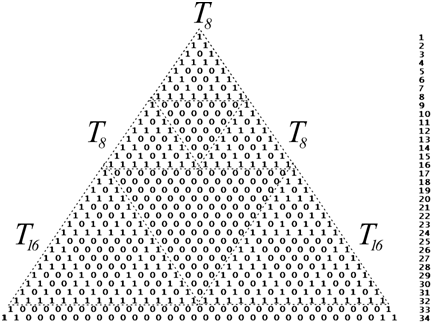
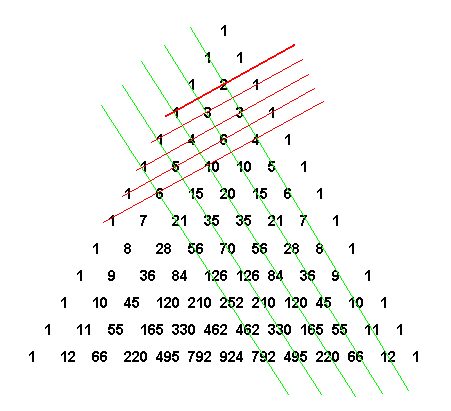
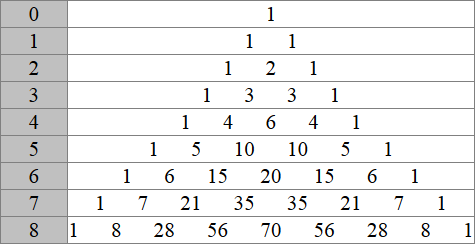
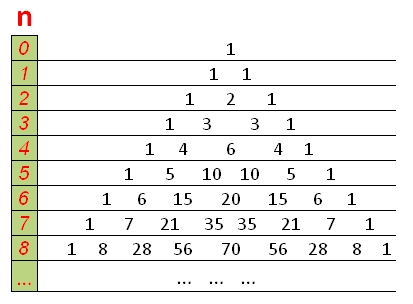
Треугольник Паскаля - это бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.
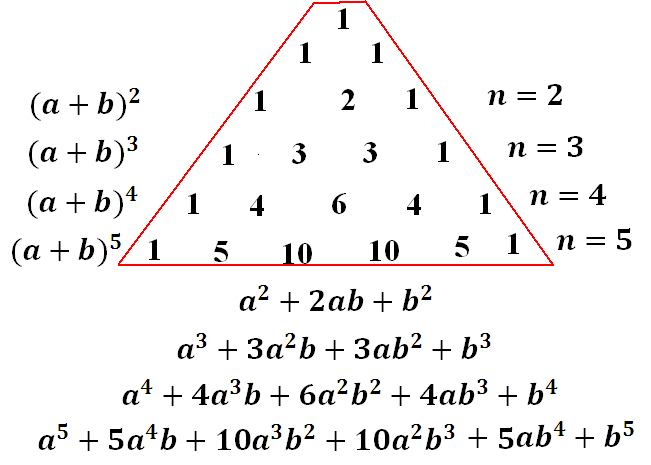
Треугольник Паскаля имеет множество свойств и особенностей. В каждой строке треугольника находятся биномиальные коэффициенты, которые представляют собой коэффициенты в разложении степени бинома Ньютона. Сумма чисел в каждой строке равна соответствующей степени двойки. Треугольник Паскаля также связан с числами Фибоначчи - суммами чисел вдоль диагоналей, идущих слева направо и снизу вверх.
Для вычисления биномиальных коэффициентов в разложении используется треугольник Паскаля. В этом треугольнике каждое число равно сумме двух чисел, стоящих над ним справа и слева в предыдущей строке. Биномиальные коэффициенты вычисляются по формуле .
См. также
Примеры
Некоторые примеры биномиальных коэффициентов в треугольнике Паскаля:
Таким образом, треугольник Паскаля является важным и полезным инструментом в математике, который находит применение в различных областях.




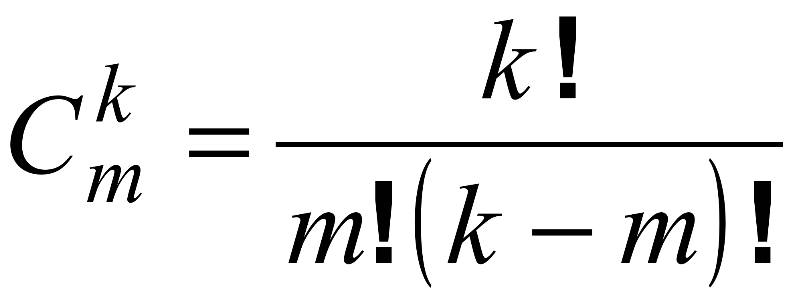
![Закономерности треугольника Паскаля . Магия математики [Как найти x и зачем это нужно]](https://storage.yandexcloud.net/wr4img/479461_i_134.png)