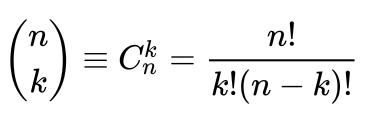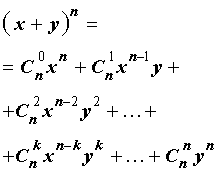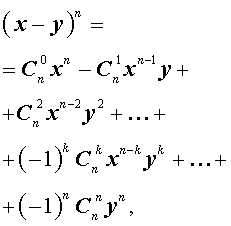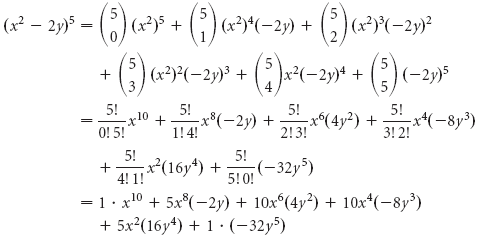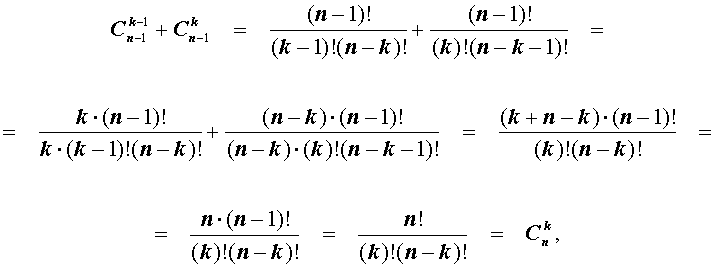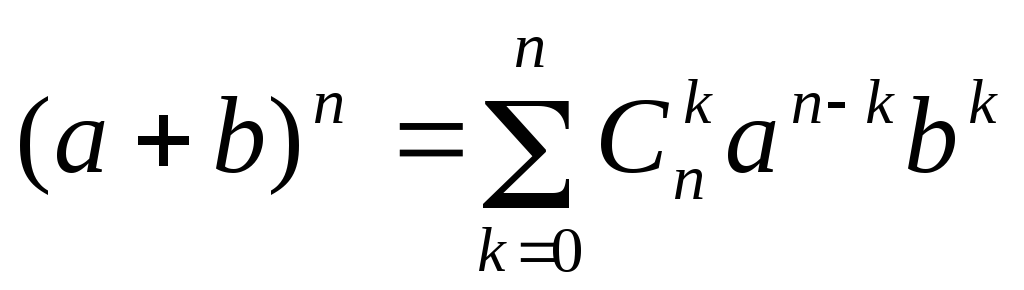Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Она имеет следующий вид: ...(Full description)
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Она имеет следующий вид:
где
( n k )
≡
C n k
=
n! k!(n-k)!
где,
n — неотрицательное целое число.
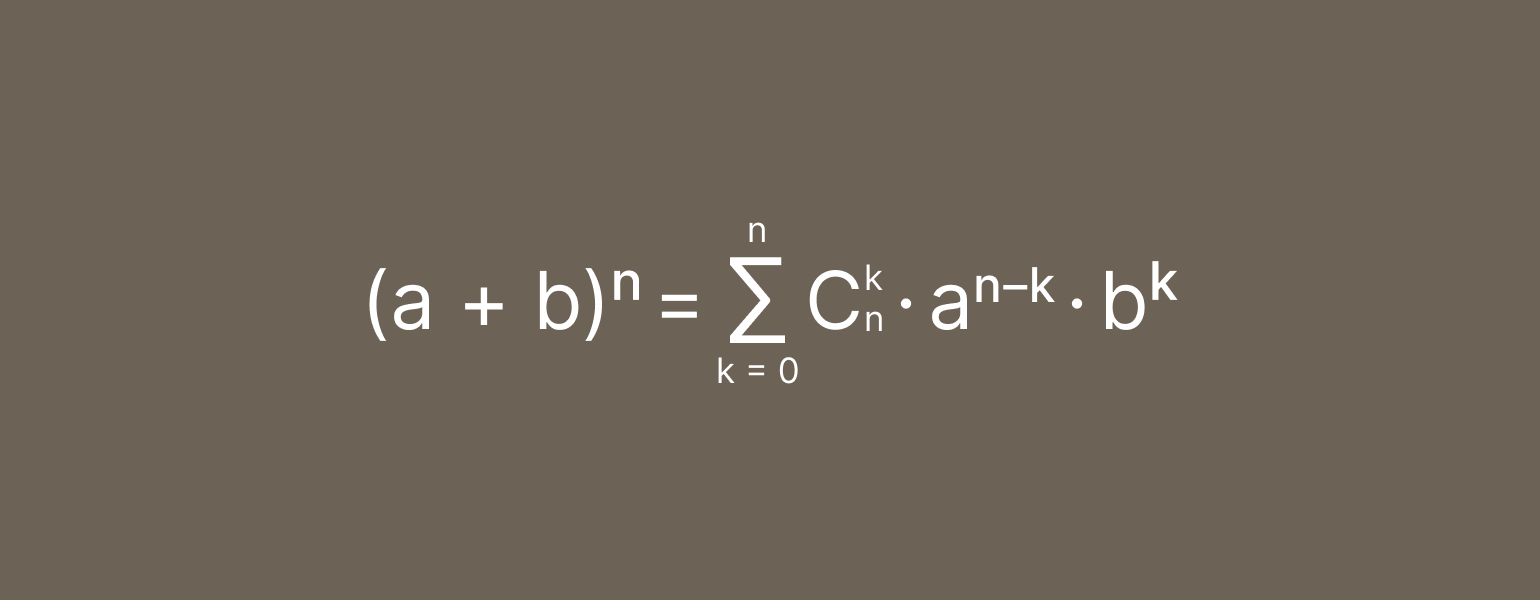
История и общий вид
Эта формула была известна ещё индийским и персидским математикам, Ньютон же вывел ее для более общего случая, когда показатель степени может быть произвольным действительным числом. Впоследствии эта формула была распространена и на комплексные числа. В общем случае бином представляет собой бесконечный ряд.
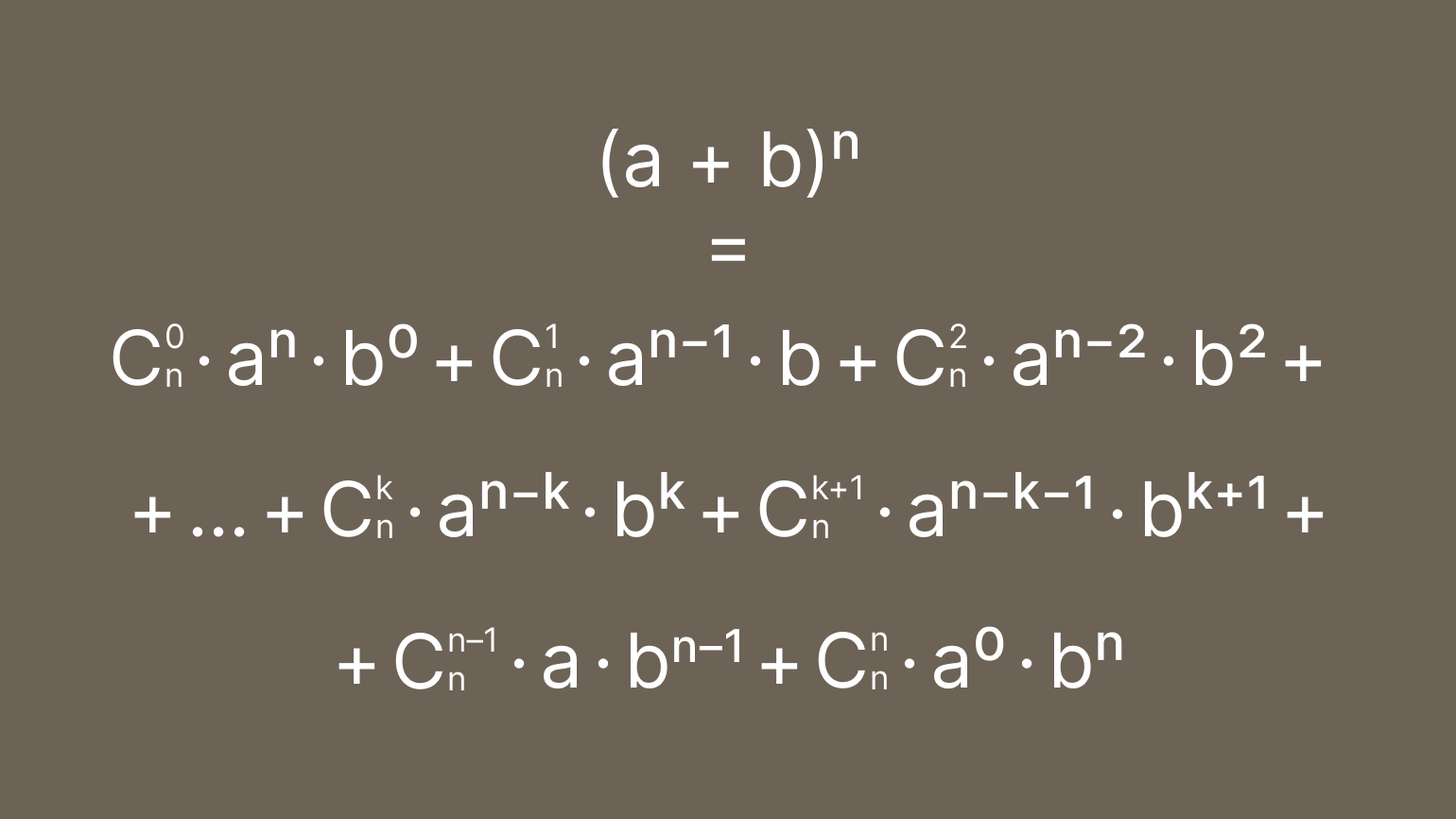
Примеры
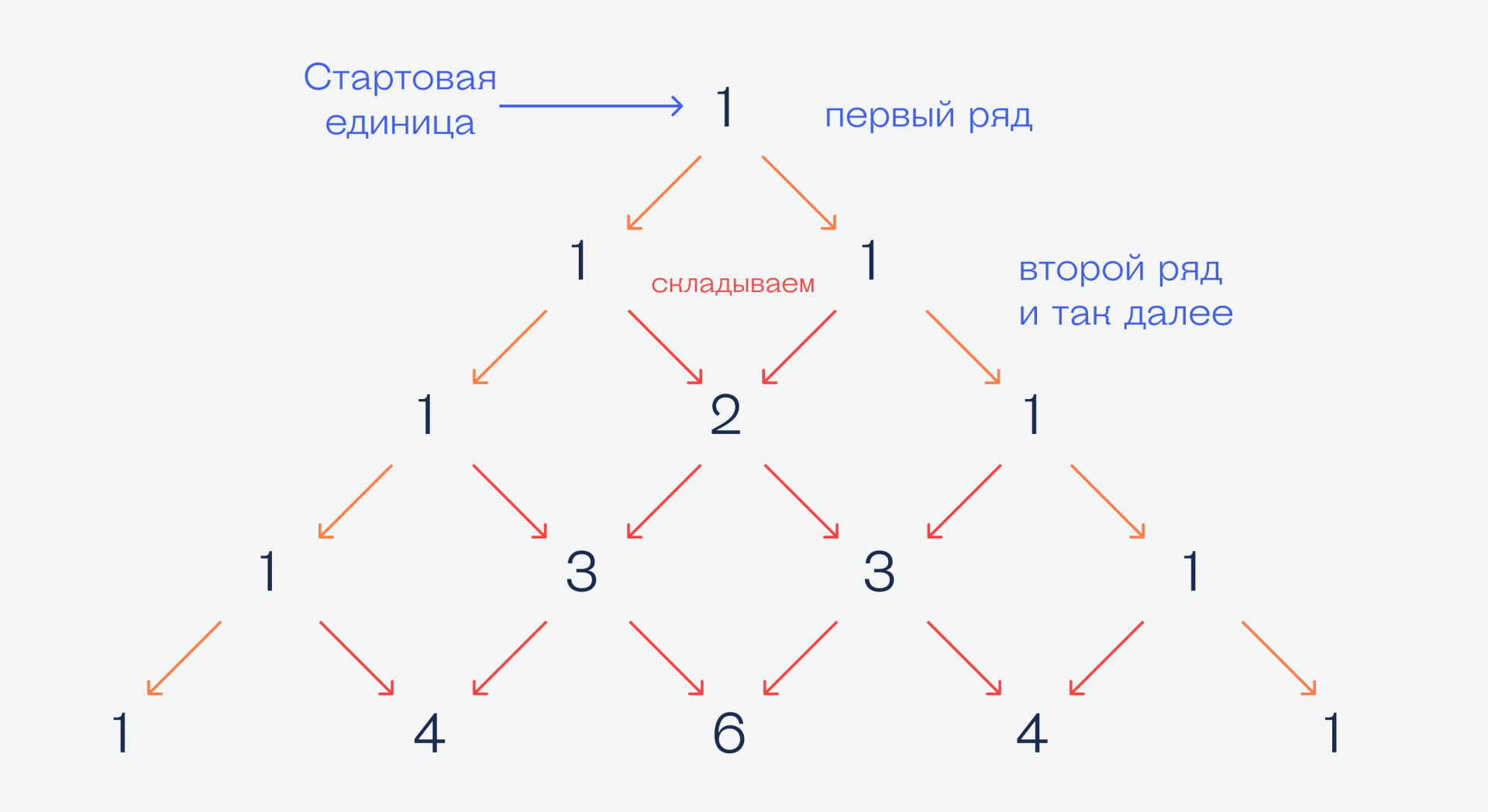
Для быстрого разложения часто пользуются треугольником Паскаля.
См. также
Доказательство
Чтобы умножить скобки, нужно взять из каждой по одному слагаемому и все полученные произведения сложить. Для получения степени a^k * b^(n-k) нужно из k скобок выбрать a, а из оставшихся (n-k) выбрать b. Вариантов выбрать a в первый раз столько же, сколько и скобок, то есть n. Затем, соответственно, n-1, и так далее до n-k+1 на k-м шаге. Однако для каждого варианта посчитаются и все его порядковые перестановки, число которых k!. Нормируя, получаем в точности C_n^k.

Треугольник Паскаля
Для быстрого разложения часто используют треугольник Паскаля. Это треугольник, в котором каждое число получается сложением двух чисел, расположенных над ним. Треугольник Паскаля позволяет находить биномиальные коэффициенты, которые используются в биноме Ньютона. Ниже представлен пример треугольника Паскаля:
| 1 | |||||
| 1 | 1 | ||||
| 1 | 2 | 1 | |||
| 1 | 3 | 3 | 1 | ||
| 1 | 4 | 6 | 4 | 1 | |
| 1 | 5 | 10 | 10 | 5 | 1 |
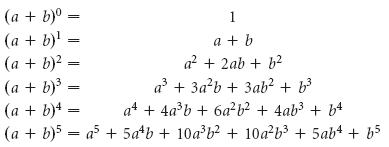
Заключение
Бином Ньютона формула является мощным инструментом для разложения на отдельные слагаемые суммы двух переменных. Она имеет широкое применение в математике и науке в целом. Использование треугольника Паскаля упрощает вычисление биномиальных коэффициентов и позволяет быстро разложить сложные выражения. Понимание и применение бинома Ньютона является неотъемлемой частью математического образования и науки.
См. также
Что нам скажет Википедия?
Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид:где ( n k ) ≡ C n k = n ! k ! ( n − k ) ! — биномиальные коэффициенты, n — неотрицательное целое число.
В таком виде эта формула была известна ещё индийским и персидским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное действительное число (позднее она была распространена и на комплексные числа). В общем случае бином представляет собой бесконечный ряд.
Примеры:
Для быстрого разложения часто пользуются треугольником Паскаля.
Чтобы умножить скобки, нужно взять из каждой по одному слагаемому и все полученные произведения сложить. Для получения степени a k b n − k нужно из k скобок выбрать a , а из оставшихся n − k выбрать b . Вариантов выбрать a в первый раз столько же, сколько и скобок, то есть n . Затем, соответственно, n − 1 , и так далее до n − k + 1 на k -м шаге. Однако для каждого варианта посчитаются и все его порядковые перестановки, число которых k ! . Нормируя, получаем в точности C n k . Ниже приводится доказательство по индукции.
Формула бинома Ньютона является частным случаем разложения функции ( 1 + x ) r в ряд Тейлора:
где r может быть произвольным комплексным числом (в частности, отрицательным или вещественным). Коэффициенты этого разложения находятся по формуле
При этом ряд ∑ k = 0 ∞ ( r ) сходится при | x | ⩽ 1 .
В частности, при x = 1 m и α = x ⋅ m получается тождество
Переходя к пределу при m → ∞ и используя второй замечательный предел lim m → ∞ ( 1 + 1 m ) m = e , выводим тождество
которое именно таким образом было впервые получено Эйлером.
Бином Ньютона может быть обобщён до полинома Ньютона — возведения в степень суммы произвольного числа слагаемых:
суть Мультиномиальные коэффициенты. Сумма берётся по всем неотрицательным целым индексам k j , сумма которых равна n (то есть по всем композициям числа n длины m ). При использовании полинома Ньютона считается, что выражения x j 0 = 1 , даже если x j = 0 .
Мультиномиальная теорема легко доказывается либо индукцией по m , либо из комбинаторных соображений и комбинаторного смысла полиномиального коэффициента.
При m = 2 , выражая k 2 = n − k 1 , получаем бином Ньютона.
Пусть B n ( a s ) = B n ( a 1 , … , a n ) и B 0 = 1 , тогда полные полиномы Белла обладают биномиальным разложением:
Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю, жившему в XIII веке, а также персидским математикам ат-Туси (XIII век) и аль-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.
Исаак Ньютон около 1665 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). На основе биномиального разложения Ньютон, а позднее Эйлер, выводили всю теорию бесконечных рядов.
В художественной литературе «бином Ньютона» часто фигурирует как синоним чего-то очень сложного (нередко иронически). Например, в романе «Мастер и Маргарита» М. А. Булгакова: «подумаешь, бином Ньютона! Умрёт он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвёртой палате».
В повести «Последнее дело Холмса» Шерлок Холмс рассказывает о профессоре Мориарти, в частности, следующее: «…когда ему исполнился 21 год, он написал трактат о биноме Ньютона, завоевавший ему европейскую известность…».