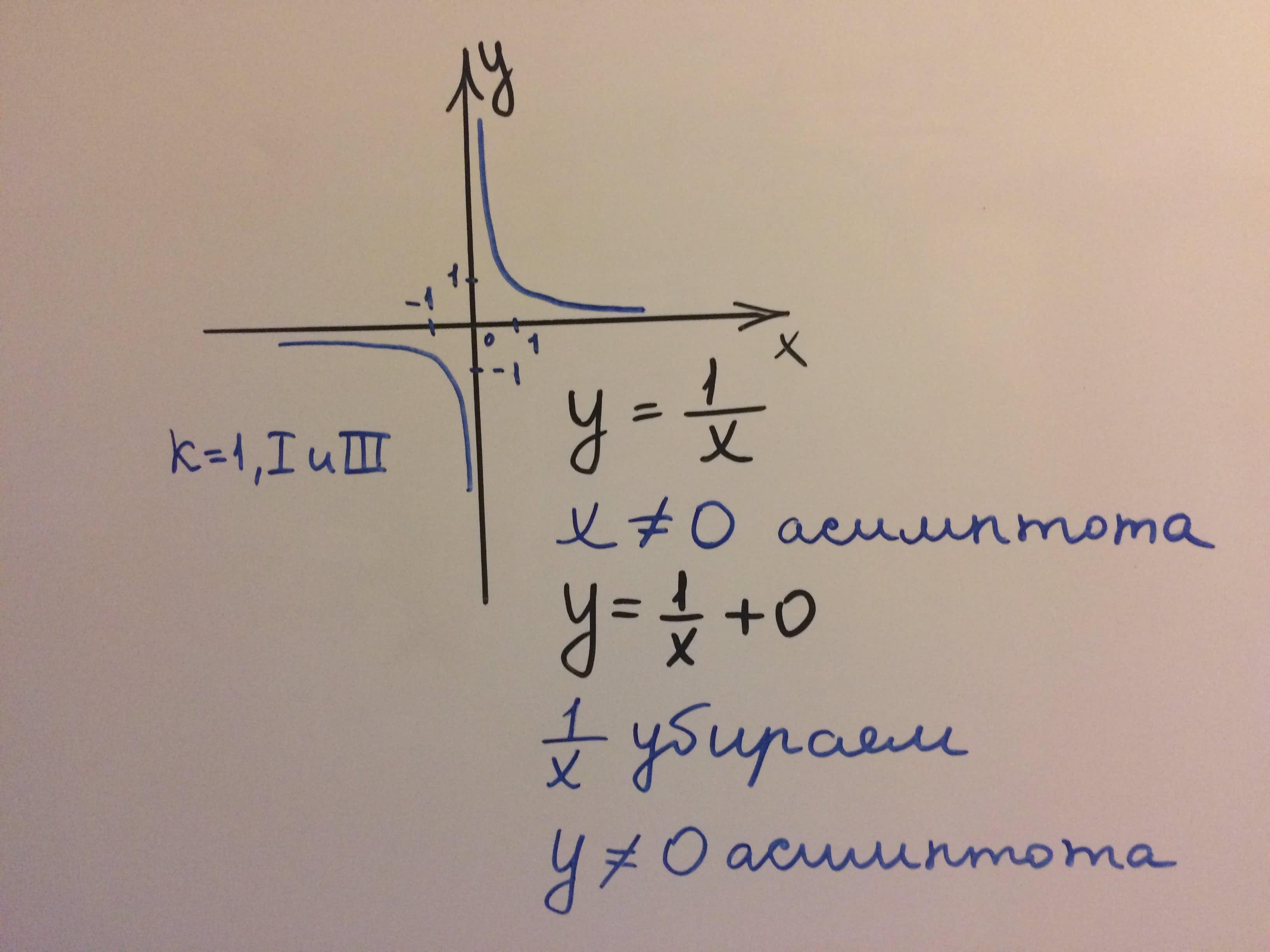Гипербола - геометрическое место точек на плоскости, которое образуется в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Она имеет две ветви и может быть определена через фокусы, директрису и фокус, а также как коническое сечение. Узнайте, почему у гиперболы две ветви и как она строится.
Гипербола (греч. ὑπερβολή) - геометрическое место точек на евклидовой плоскости, для которых абсолютное значение разности расстояний от точки M до двух фокусов F1 и F2 постоянно. Гипербола является коническим сечением и квадрикой, наряду с эллипсом и параболой.
История
Термин "гипербола" был введен Аполлонием Пергским в 3 веке до н.э. Задача о построении точек гиперболы сводится к задаче о приложении с избытком.

Определения
Коническое сечение
Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также вырожденные случаи, такие как пересекающиеся и совпадающие прямые и точка, возникающие, когда плоскость проходит через вершину конуса. Пересекающиеся прямые могут считаться вырожденной гиперболой, совпадающей со своими асимптотами.
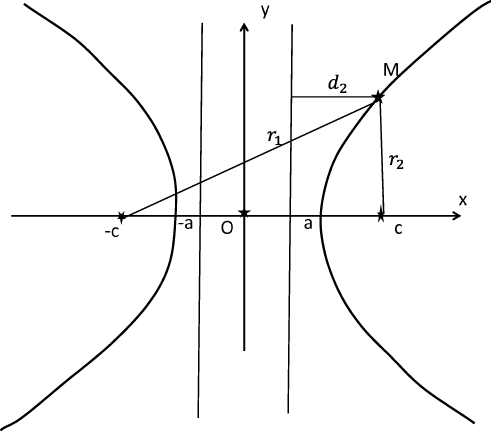
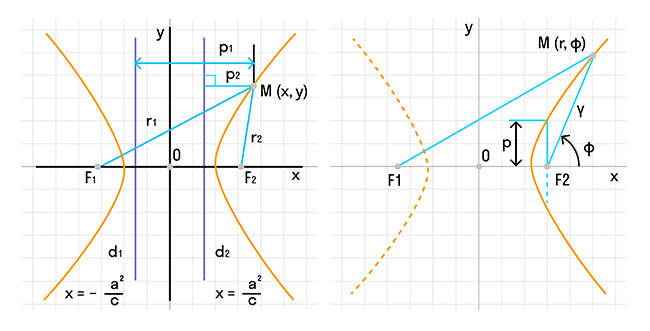
Через фокусы
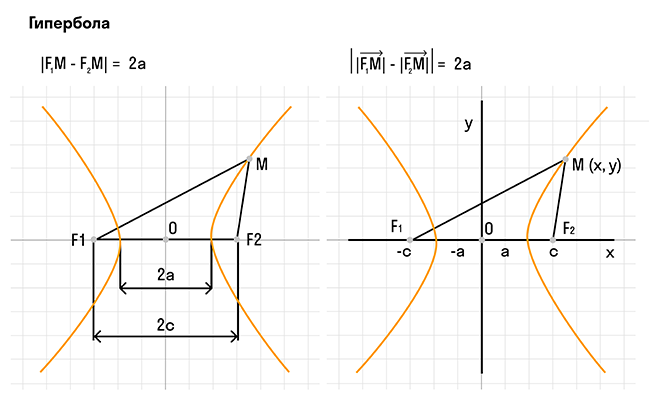
Гипербола может быть определена как геометрическое место точек, для которых абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Через директрису и фокус
Гипербола может быть определена как геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы. Эксцентриситет гиперболы определяется постоянной ε > 1.
Связанные определения
Гипербола - это множество точек на плоскости, для которых модуль разности расстояний от двух точек (фокусов) является величиной постоянной и меньшей, чем расстояние между фокусами.
См. также
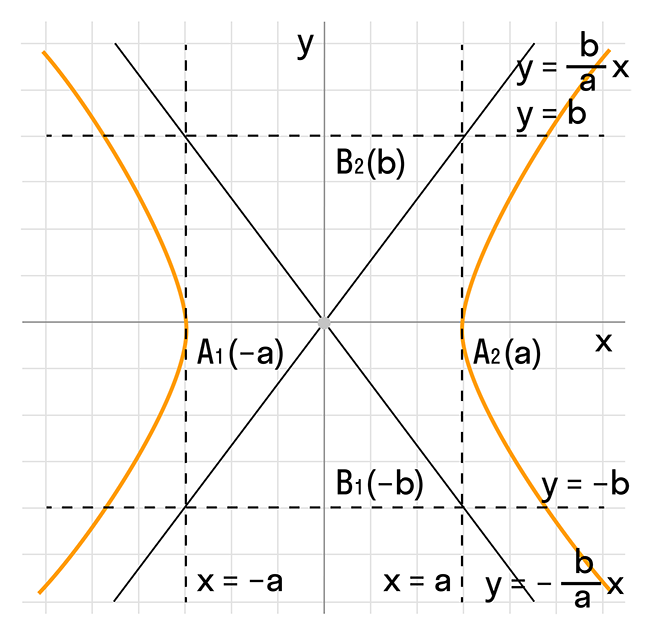
Форма гиперболы
Гипербола симметрична относительно центра О, который является серединой отрезка, соединяющего фокусы F' и F. Прямые F'F и Y'Y, перпендикулярные F'F и проходящие через О, также являются осями симметрии гиперболы. Вершины гиперболы находятся на прямых F'F и F'F и обозначаются как A и A'. Расстояние между вершинами образует действительную ось гиперболы. Мнимая ось гиперболы образуется на прямой Y'Y и обозначается как B'B.
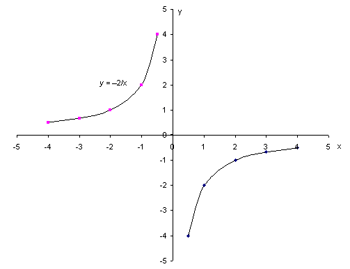
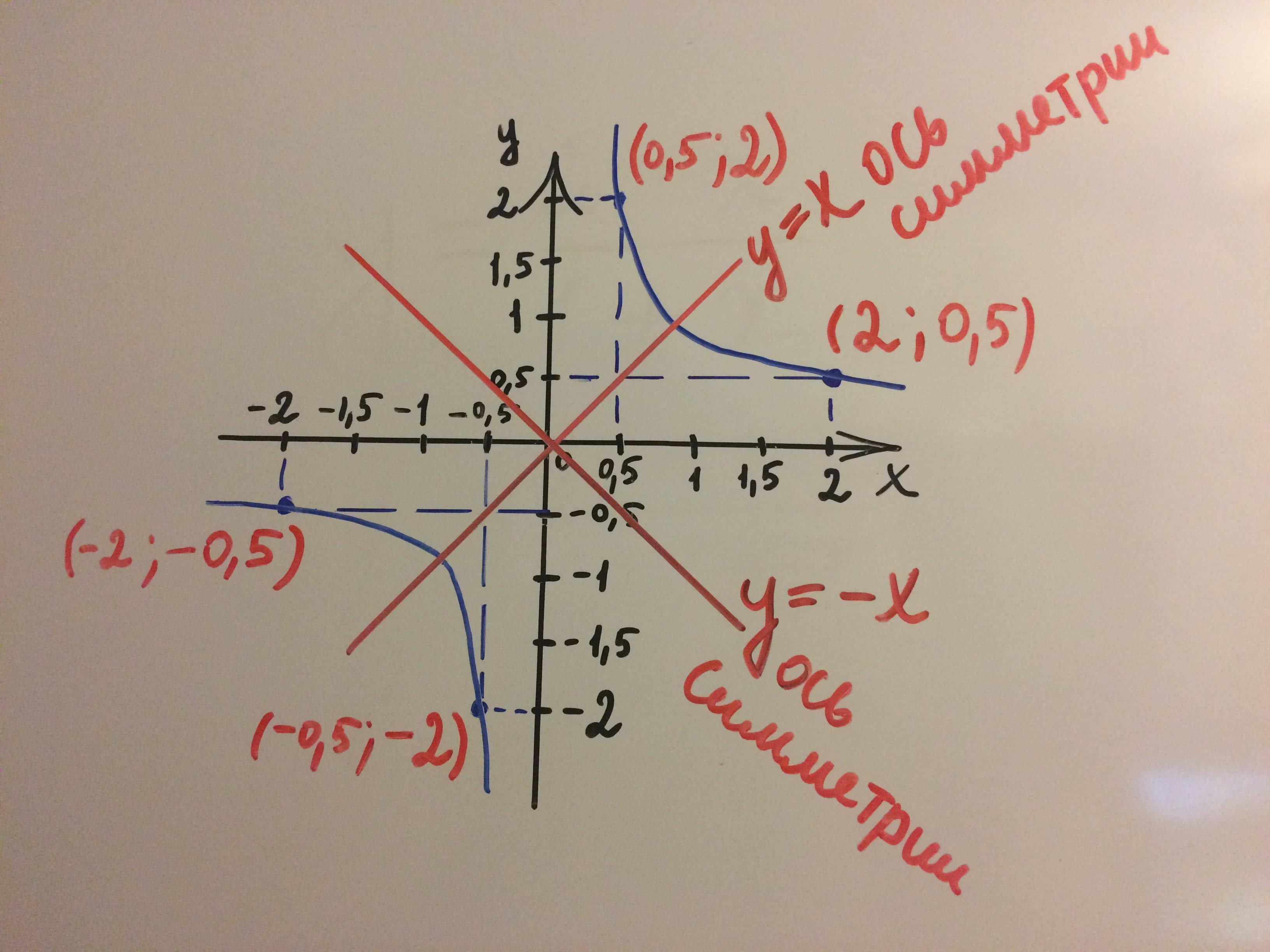
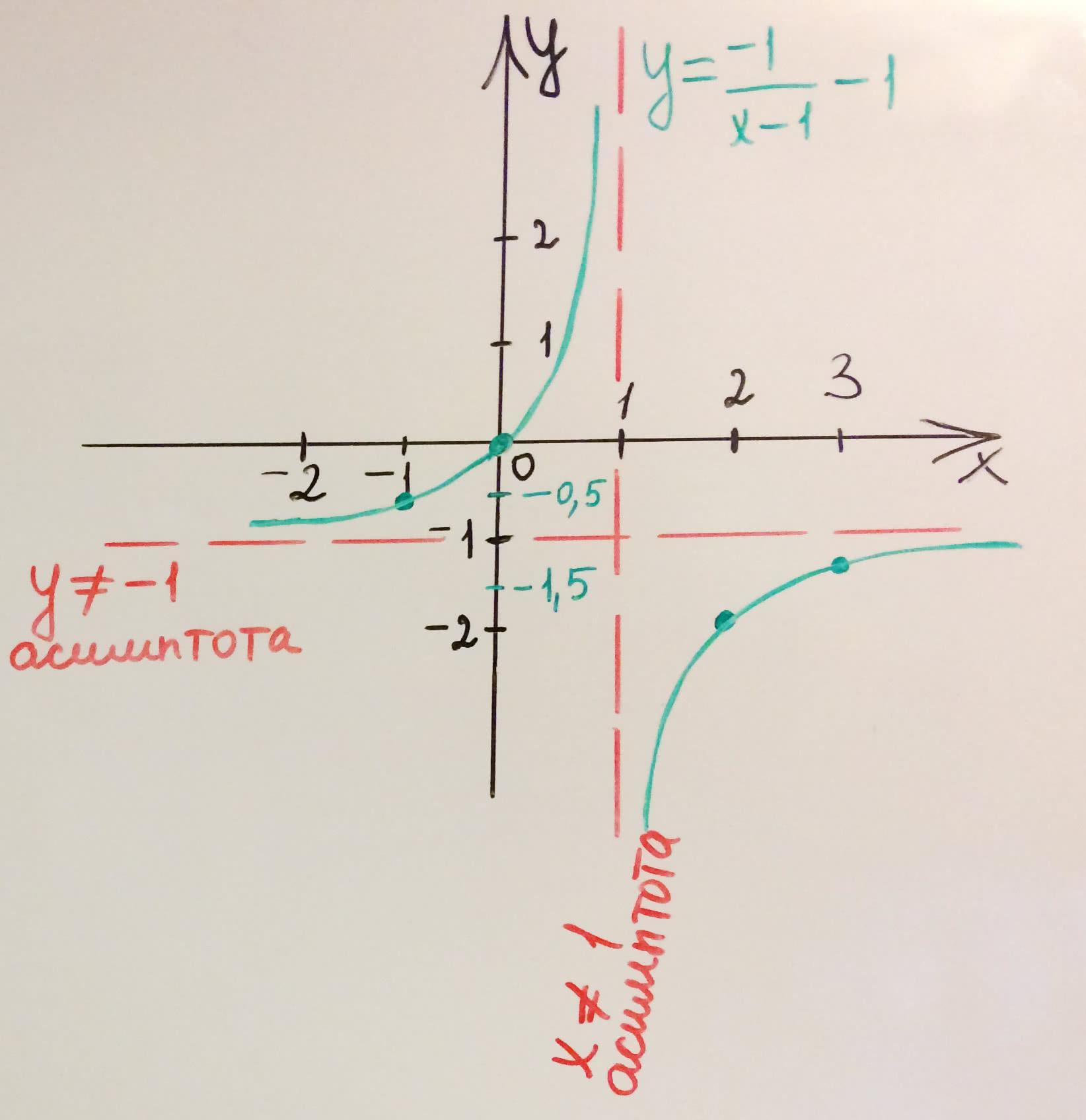
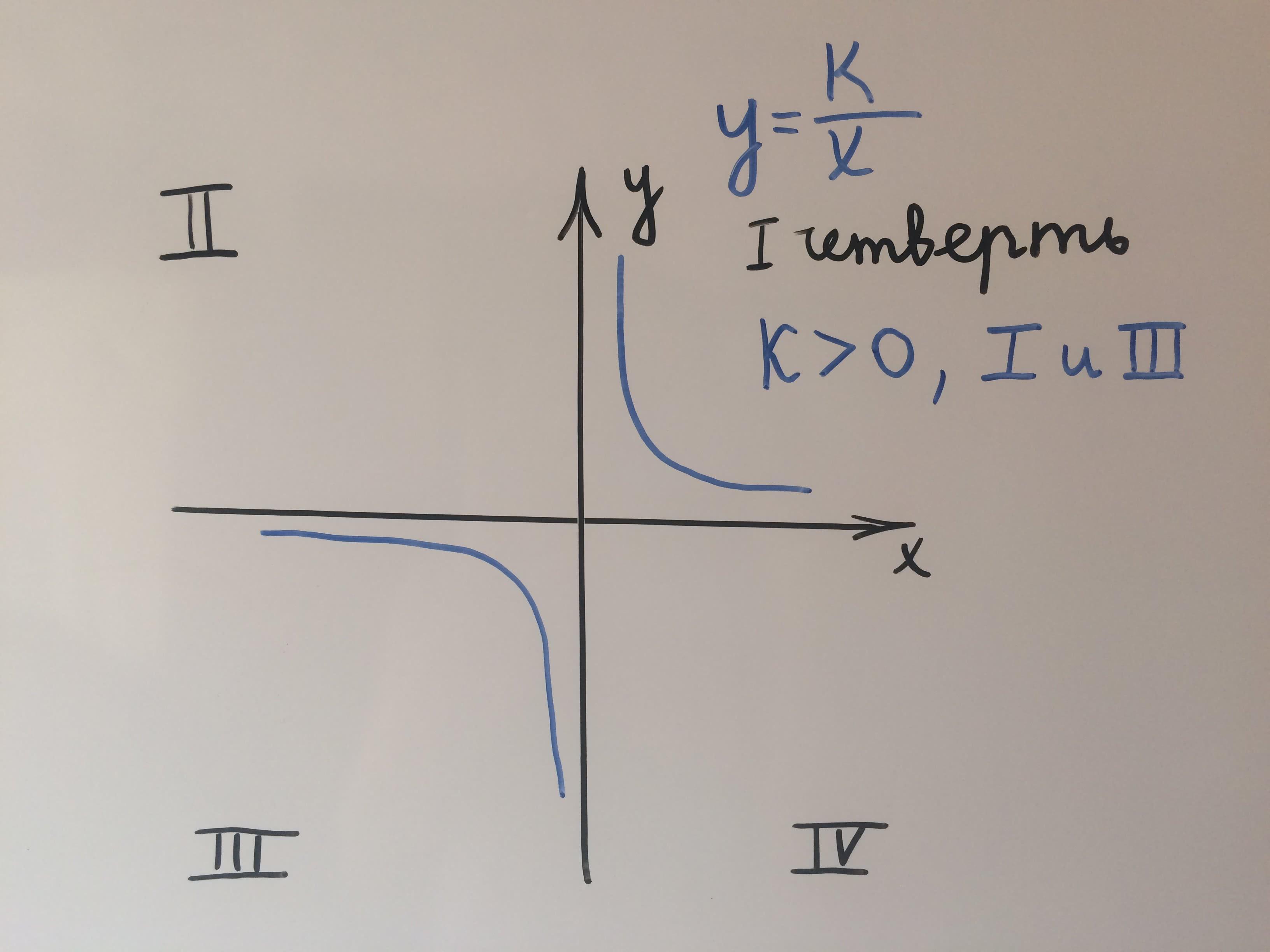
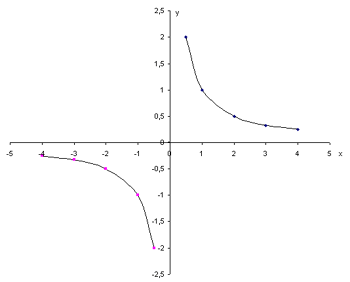
Математическое уравнение гиперболы имеет вид y = k/x, где k - коэффициент обратной пропорциональности. Гипербола может иметь две ветви, которые находятся в разных четвертях, в зависимости от знака коэффициента k.
Построение гиперболы
Построение гиперболы может осуществляться с использованием канонического уравнения гиперболы или измененного уравнения для каждого конкретного случая.
Пример 1. Построение гиперболы, заданной уравнением 5(x^2) - 4(y^2) = 20:
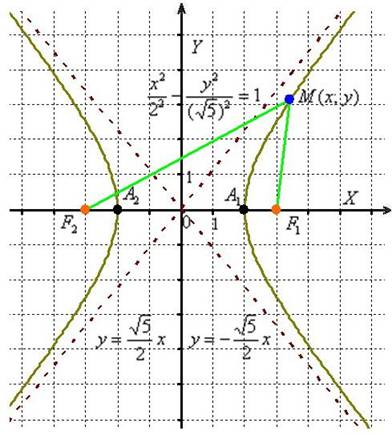
Можно упростить уравнение, разделив обе части на 20: (x^2)/4 - (y^2)/5 = 1. В данном примере действительная полуось а равна 2, мнимая полуось b равна √5, а расстояние между вершинами гиперболы равно 4.
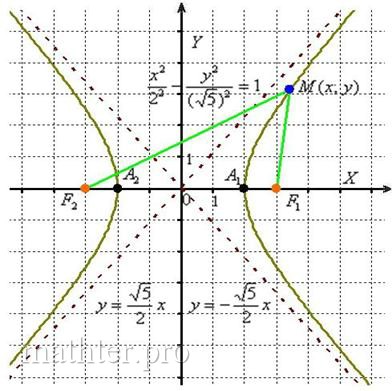
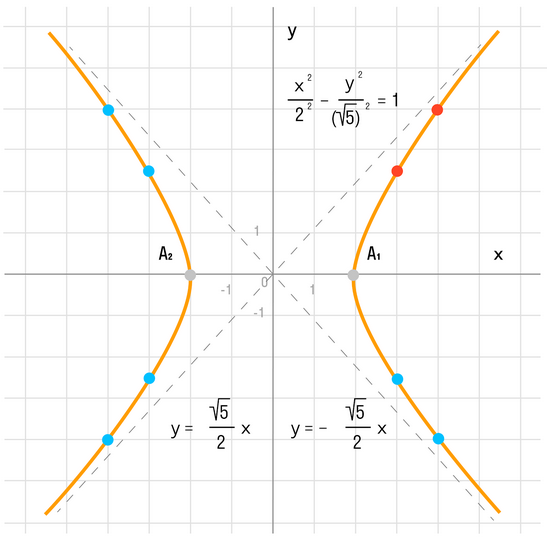
Пример 2. Построение гиперболы, заданной уравнением 3(x^2)/20 - 8(y^2)/20 = 1:
В данном примере действительная полуось а равна 2, мнимая полуось b может быть вычислена и имеет значение √5/2. Действительная ось гиперболы представляет собой отрезок А1А2, а мнимая ось - отрезок B'B.
Заключение
Гипербола - это одно из конических сечений и квадрик в геометрии. У гиперболы всегда две ветви, которые могут быть определены разными способами, включая через фокусы, через директрису и фокус, а также как коническое сечение. Гипербола имеет определенную форму, симметричную относительно центра и осей симметрии, а ее уравнение может быть задано с помощью канонической формы или измененной формы для каждого конкретного случая.
См. также
Что нам скажет Википедия?
Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Для сравнения: кривая постоянной суммы расстояний от любой её точки до фокусов — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.
Через директрису и фокус
Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная ε > 1 {\displaystyle \varepsilon >1} называется эксцентриситетом гиперболы.