Узнайте, какие стороны тетраэдра равны и изучите его основные характеристики, свойства и математические характеристики. Правильный и равнобедренный тетраэдр в геометрии.
Cодержание
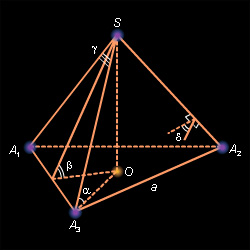
Тетраэдр является частным случаем пирамиды, где все его грани являются треугольниками, включая основание пирамиды. Этот трехмерный многогранник имеет четыре грани и называется "тетраэдр", что происходит от греческого слова "tetra", означающего "четыре". В данной статье мы рассмотрим различные аспекты тетраэдра, включая равные стороны и другие свойства.
Основные характеристики тетраэдра
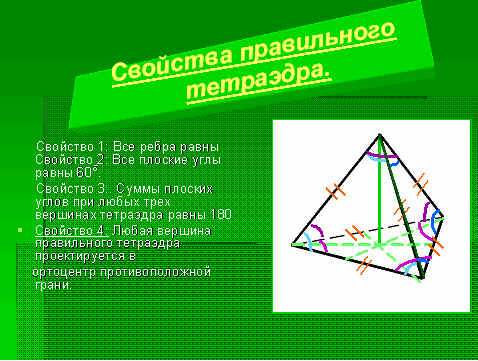
Тетраэдр представляет собой полиэдр, у которого все грани являются треугольниками. У правильного тетраэдра все четыре треугольные грани равны и все внутренние углы равны 60 градусов. Все вершины тетраэдра лежат на одной сфере, называемой описанной сферой.
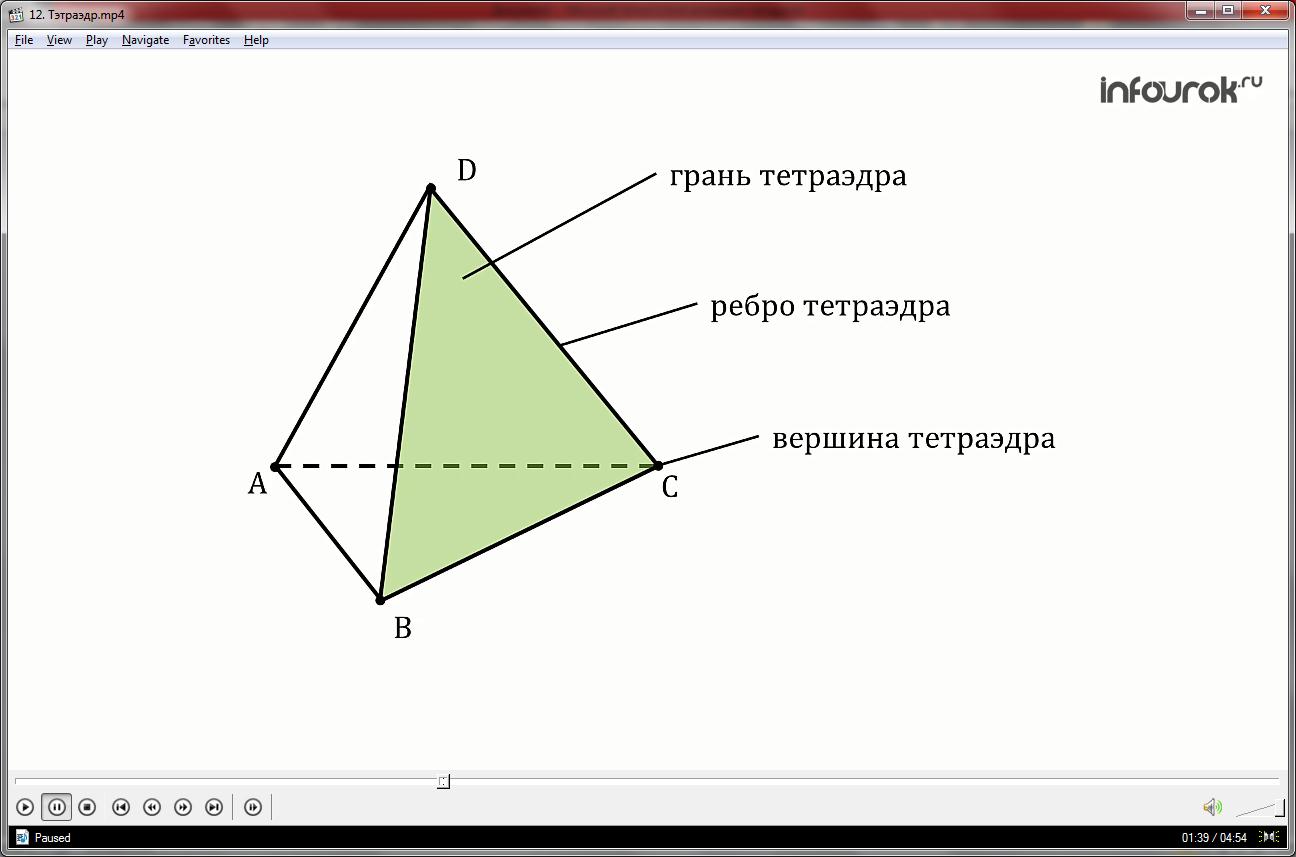
Равные стороны тетраэдра
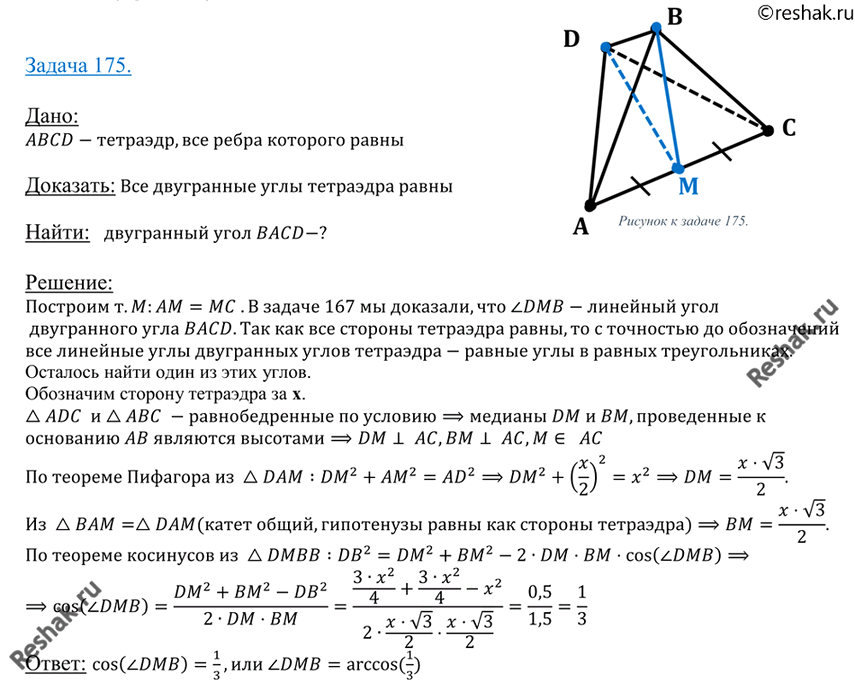
У равнобедренного тетраэдра все четыре грани равны. Это означает, что длины всех сторон равны друг другу. Равнобедренный тетраэдр может иметь различные конфигурации, где основание может быть любой из четырех граней.
Правильный тетраэдр
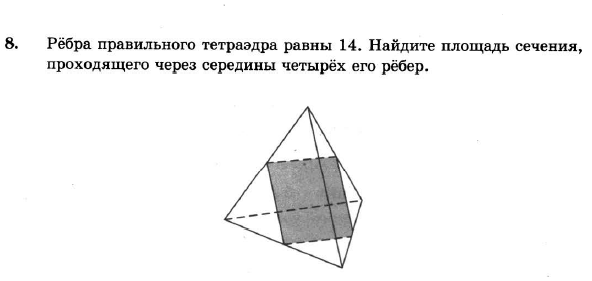
Правильный тетраэдр является частным случаем равнобедренного тетраэдра, где все четыре грани являются равносторонними треугольниками. Такой тетраэдр имеет равные стороны и углы. В правильном тетраэдре все внутренние углы равны 60 градусов.
См. также
Другие свойства тетраэдра
У тетраэдра есть несколько других интересных свойств:
- Все внутренние углы тетраэдра составляют 180 градусов.
- Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
- У правильного тетраэдра каждая медиана совпадает с осью симметрии.
- Расширенный тетраэдр состоит из обычного тетраэдра и описывающей его сферы.

Математические характеристики тетраэдра
Для тетраэдра существуют различные математические характеристики:
- Радиус описанной сферы тетраэдра определяется по формуле: R = a / (3√2), где a - длина стороны.
- Радиус вписанной сферы тетраэдра определяется по формуле: r = a / (6√6).
- Площадь поверхности тетраэдра можно определить как площадь одной из сторон, умноженную на 4.
- Объем тетраэдра определяется по формуле: V = (a^3) / (6√2).
Заключение
Тетраэдр - это геометрическая фигура, у которой все грани являются треугольниками. Равнобедренный тетраэдр имеет равные стороны, а правильный тетраэдр имеет равные стороны и углы. У тетраэдра есть много интересных свойств и математических характеристик, которые делают его важным объектом изучения в геометрии.