Тетраэдр является частным случаем пирамиды, где все его грани являются треугольниками, включая основание пирамиды. Узнайте свойства и особенности тетраэдра и что равно в нем. Возможности использования медиан тетраэдра для решения геометрических задач.
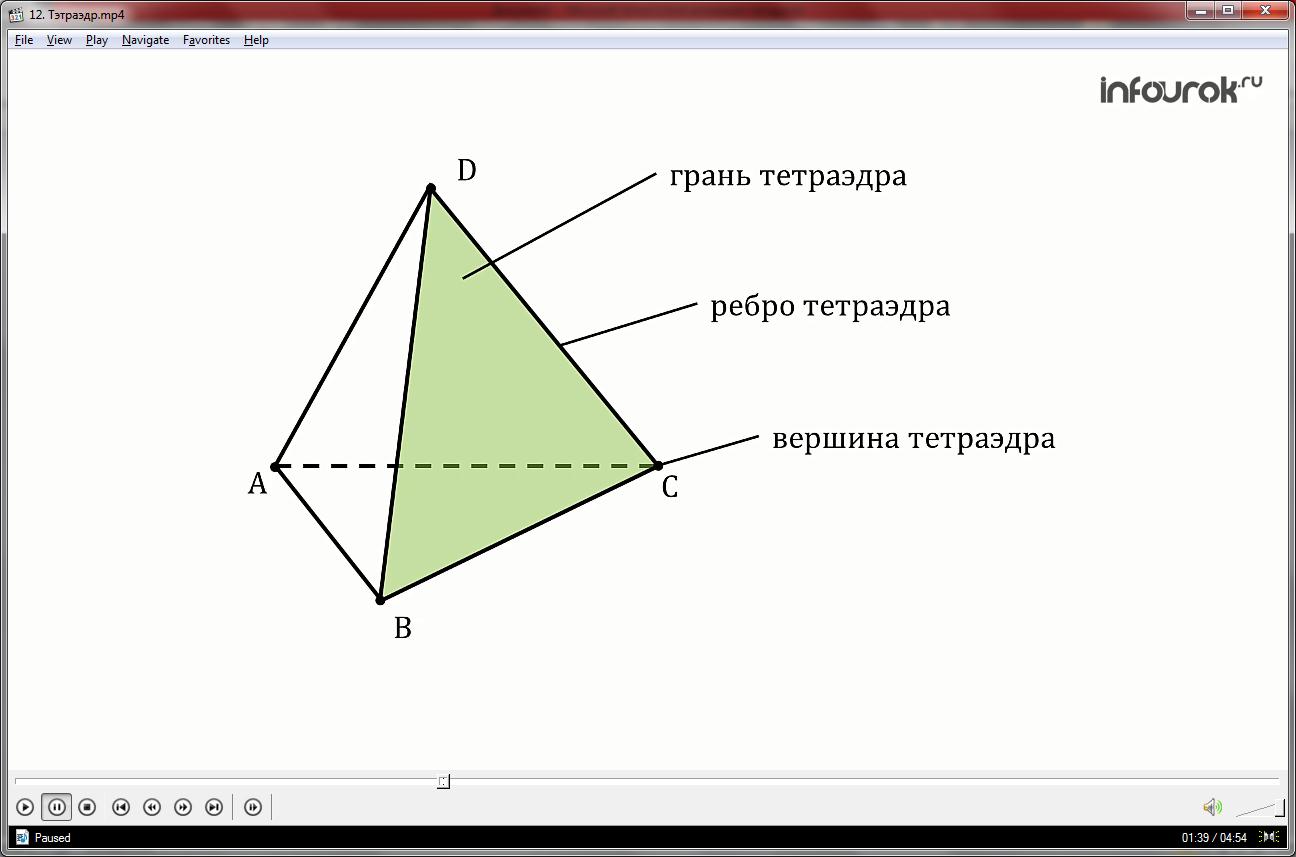
Тетраэдр является частным случаем пирамиды, где все его грани являются треугольниками, включая основание пирамиды. Этот многогранник представляет собой трехмерную геометрическую форму с плоскими гранями и прямыми ребрами. Слово "тетра" происходит из греческого языка и означает "четыре", так как у тетраэдра есть 4 грани.
Свойства тетраэдра
Тетраэдр имеет следующие свойства:
- Тетраэдр всегда имеет треугольное основание, и любая из четырех его граней может быть обозначена как основание, если он правильный.
- Все грани тетраэдра являются треугольниками, включая основание.
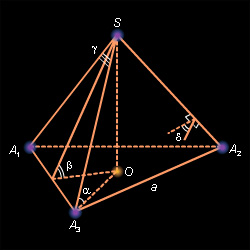
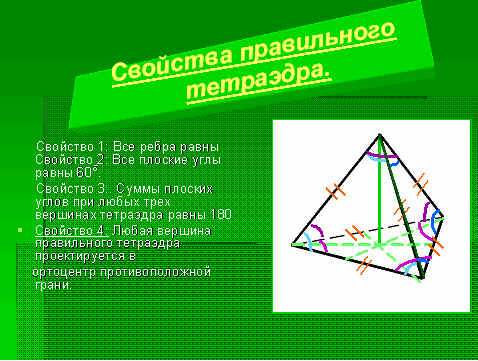
- Правильный тетраэдр является частным случаем тетраэдра, в котором все четыре треугольные грани равны, а все внутренние углы равны. На рисунке ниже показан равнобедренный тетраэдр.
Поскольку все грани правильного тетраэдра являются равносторонними треугольниками, все внутренние углы тетраэдра будут составлять 60 градусов, а сумма углов граней, встречающихся в любой вершине, будет равна 180 градусов. Тетраэдр имеет четыре медианы, которые являются осью симметрии.
Расширенный тетраэдр
В математике существует понятие расширенного тетраэдра, который состоит из обычного тетраэдра и сферы, описывающей его грани. Расширенный тетраэдр имеет несколько интересных свойств и применений в различных областях науки.
Медиана тетраэдра
Медиана является одной из наиболее важных характеристик тетраэдра. Она представляет собой отрезок, соединяющий вершину тетраэдра с серединой противолежащей грани.
Одно из свойств медианы заключается в том, что она делит другие медианы тетраэдра в определенной пропорции. Для любого тетраэдра верно соотношение: длина медианы ак = длина отрезка, соединяющего середины других медиан, деленная на 3.
Это свойство позволяет использовать медианы для решения геометрических задач и нахождения неизвестных величин в тетраэдре.
Заключение
Тетраэдр является многогранником с плоскими гранями, прямыми ребрами и треугольным основанием. В правильном тетраэдре все грани равны, все внутренние углы равны и у него есть четыре медианы. Расширенный тетраэдр имеет интересные свойства и применения. Медианы тетраэдра делят другие медианы в определенной пропорции, что позволяет использовать их для решения геометрических задач.