Пра́вильный додекаэдр - один из пяти возможных правильных многогранников. Изучите историю додекаэдра, его описание и характеристики, а также способы изготовления и сборки этого уникального геометрического объекта. Узнайте о римских додекаэдрах и их загадочном назначении.
Cодержание
Введение
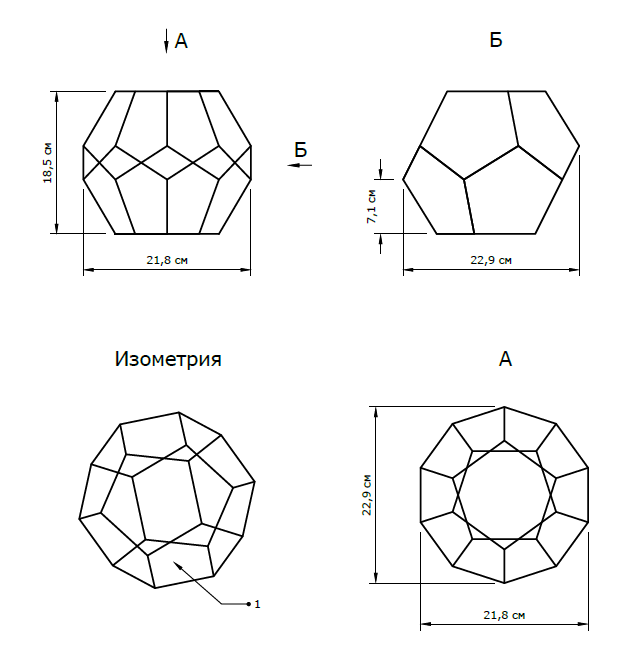
Пра́вильный додека́эдр (др.-греч. δωδεκάεδρον, от δώδεκα — «двенадцать» и ἕδρα — «грань») — один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников[1], являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).

История
Пожалуй, самый древний предмет в форме додекаэдра был найден в северной Италии, около Падуи, в конце XIX века, он датируется 500 г. до н. э. и предположительно использовался этрусками в качестве игральной кости[2][3].
Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца»[4]. Евклид в предложении 17 книги XIII «Начал» строит додекаэдр на рёбрах куба[5][6]:132-136. Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях[7][6]:318-319[8].
На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами, относящихся ко II—III вв. н. э., назначение которых не совсем понятно.
Вскоре после появления кубика Рубика, в 1981 году была запатентована подобная головоломка в форме правильного додекаэдра — мегаминкс. Как и у классического кубика Рубика, к каждому ребру у неё прилегает по три детали[9]. Позднее, как и для кубика Рубика появились такие додекаэдрические головоломки с четырьмя деталями при ребре (гигаминкс), пятью (тераминкс) и т.д. Сложность и время сборки их, как и для кубика Рубика возрастает по мере увеличения числа деталей при ребре.

Описание и характеристики
Додекаэдр представляет собой многогранник, состоящий из двенадцати правильных пятиугольников в качестве граней. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Общее количество граней составляет 12, количество рёбер - 30, а количество вершин - 20 (в каждой вершине сходятся 3 ребра).
См. также
Формулы и характеристики
Ниже представлены основные формулы и характеристики додекаэдра:
| Площадь поверхности | Формула |
|---|---|
| Объём | Формула |
| Радиус описанной сферы | Формула |
| Радиус полувписанной сферы | Формула |
| Радиус вписанной сферы | Формула |

Изготовление и сборка
Додекаэдр можно изготовить самостоятельно из бумаги или картона. Для сборки потребуется бумажная развёртка - единая деталь с линиями сгибов. Развертки можно скачать и распечатать на листе формата А4. Кроме того, существуют различные варианты окраски додекаэдра, где каждая соседняя грань окрашена в свой цвет или используется определенное количество цветов раскраски.
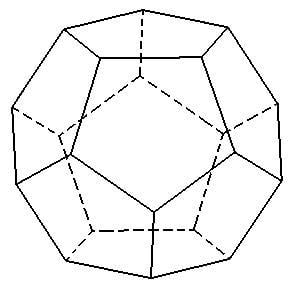
Римский додекаэдр
Римский додекаэдр — это небольшой объект, сделанный из бронзы или реже из камня или железа, чаще имеющий форму додекаэдра с двенадцатью плоскими пятиугольными гранями. Римский додекаэдр датируется II—III веком н. э. Около сотни додекаэдров было найдено на территории различных стран, но большинство из них было найдено в Германии и Франции. Назначение этих объектов до сих пор остаётся загадкой.
См. также
Заключение
Додекаэдр является одним из пяти возможных правильных многогранников и имеет множество интересных свойств и особенностей. Он привлекал внимание ученых и математиков на протяжении многих веков и использовался как символ и в различных играх и головоломках. Несмотря на множество исследований, некоторые аспекты додекаэдра до сих пор остаются загадкой.

Что нам скажет Википедия?
Пра́вильный додека́эдр (др.-греч. δωδεκάεδρον, от δώδεκα — «двенадцать» и ἕδρα — «грань») — один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников[1], являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
Пожалуй, самый древний предмет в форме додекаэдра был найден в северной Италии, около Падуи, в конце XIX века, он датируется 500 г. до н. э. и предположительно использовался этрусками в качестве игральной кости[2][3].
Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца»[4]. Евклид в предложении 17 книги XIII «Начал» строит додекаэдр на рёбрах куба[5][6]:132-136. Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях[7][6]:318-319[8].
На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами, относящихся ко II—III вв. н. э., назначение которых не совсем понятно.
Вскоре после появления кубика Рубика, в 1981 году была запатентована подобная головоломка в форме правильного додекаэдра — мегаминкс. Как и у классического кубика Рубика, к каждому ребру у неё прилегает по три детали[9]. Позднее, как и для кубика Рубика появились такие додекаэдрические головоломки с четырьмя деталями при ребре (гигаминкс), пятью (тераминкс) и т.д. Сложность и время сборки их, как и для кубика Рубика возрастает по мере увеличения числа деталей при ребре.