Узнайте, что такое гипербола в физике, ее определение, свойства и применение в различных областях. Гипербола является важной кривой, которая возникает при изучении различных физических явлений.
Cодержание
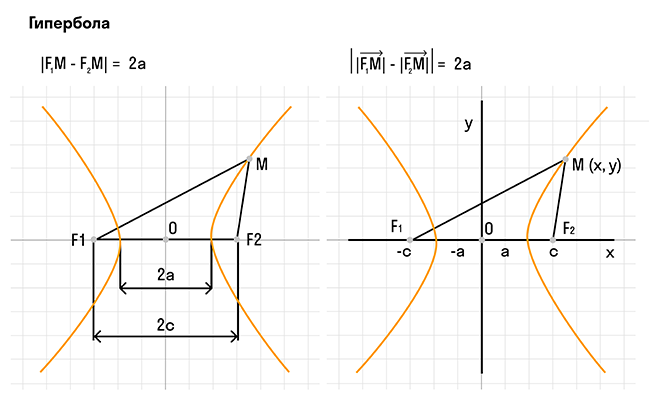
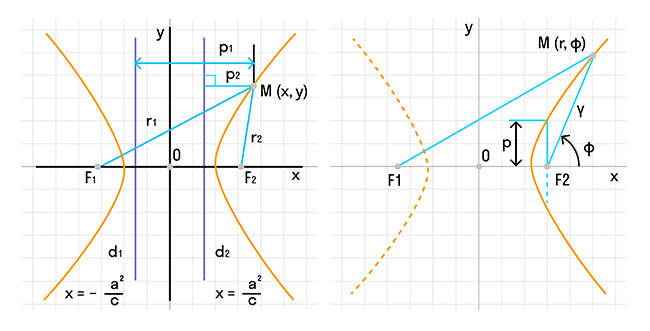
В физике гипербола является одной из важных кривых, которая возникает при рассмотрении различных физических явлений. Гипербола является одним из трех конических сечений, вместе с эллипсом и параболой. Она может быть определена как множество точек на плоскости, для которых модуль разности расстояний от двух фокусов постоянен.
История и определения гиперболы
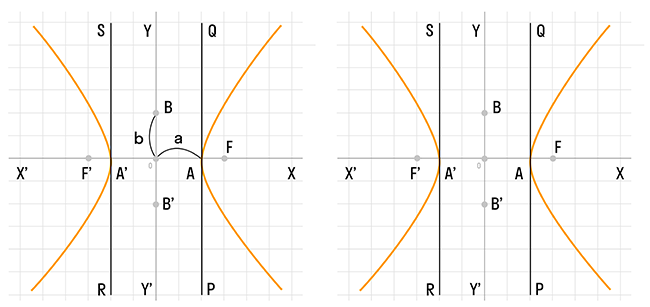
Термин "гипербола" был введен древнегреческим математиком Аполлонием Пергским в III веке до н.э. Он заметил, что задача построения точки гиперболы сводится к задаче о приложении с избытком.
Гипербола может быть определена несколькими способами. Одним из способов является определение через фокусы, где гипербола представляет собой геометрическое место точек, для которых абсолютная величина разности расстояний до фокусов постоянна. Также гиперболу можно определить как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса.
Свойства гиперболы
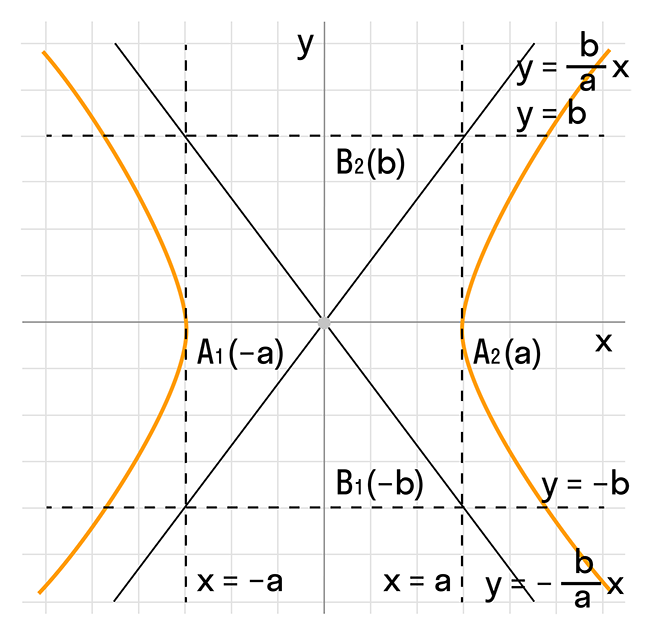
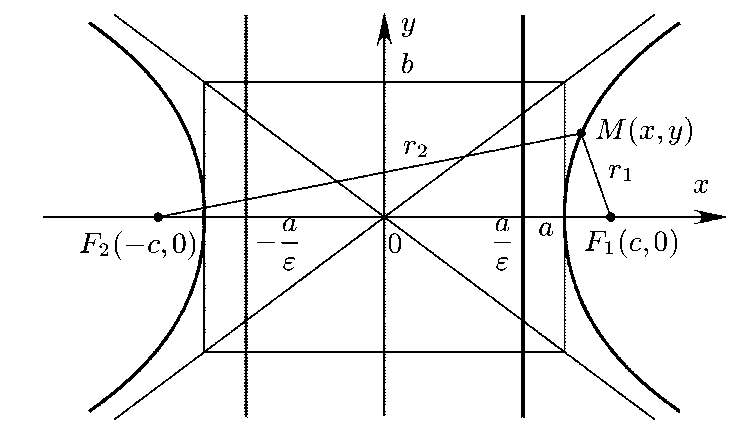
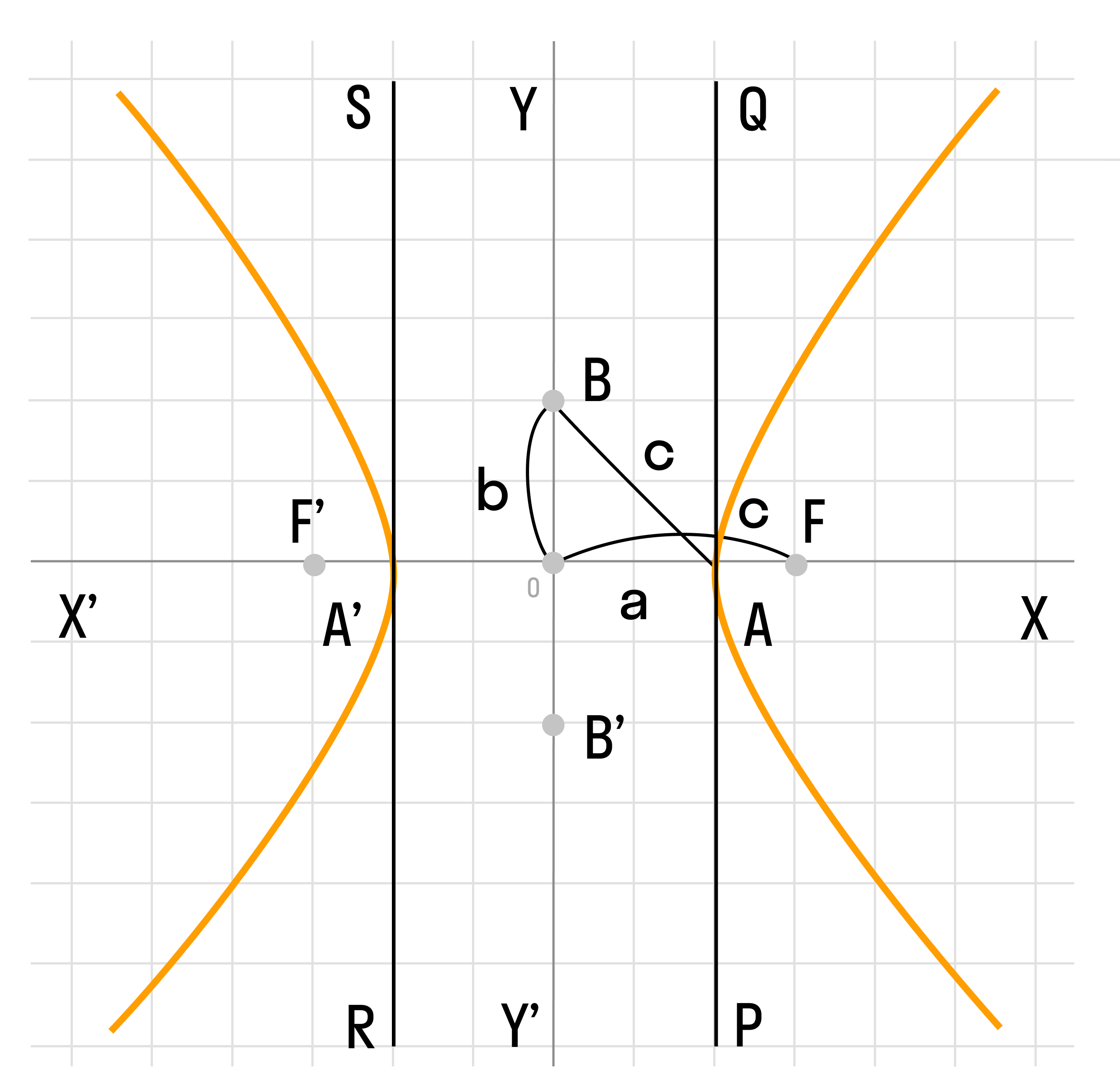
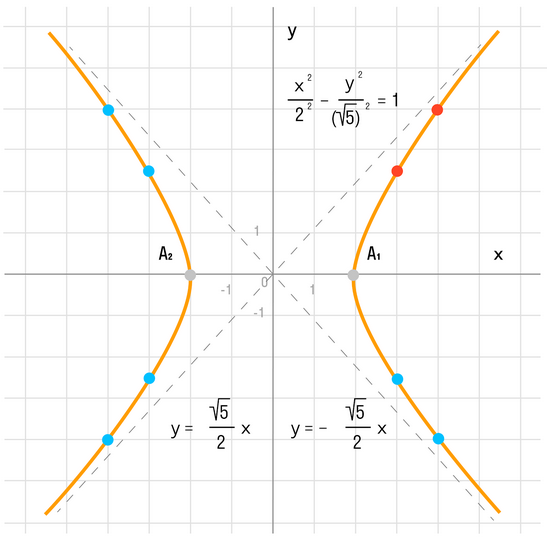
Гипербола обладает некоторыми особыми свойствами. Одно из них заключается в том, что действительная ось гиперболы — это отрезок между вершинами, где расстояние между вершинами равно двум действительным полуосям. Мнимая ось гиперболы находится на прямой, проходящей через центр гиперболы и перпендикулярной действительной оси.
Каноническое уравнение гиперболы в алгебре выглядит как y = ±(b/a) * √(x^2 - a^2), где a и b – положительные действительные числа. Здесь a является действительной полуосью гиперболы, а b – мнимой полуосью.
См. также
Применение гиперболы в физике
Гипербола находит применение в различных физических явлениях. Например, в оптике гиперболические зеркала используются для фокусировки света и создания изображений. Гиперболический потенциал в гравитационной физике описывает движение тел под действием гравитационного поля.
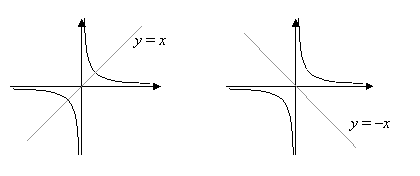
Также гипербола может быть использована в анализе электрических цепей, особенно в задачах с переменным током. Гиперболические функции, такие как гиперболический синус и гиперболический косинус, возникают при решении уравнений и моделировании различных физических процессов.
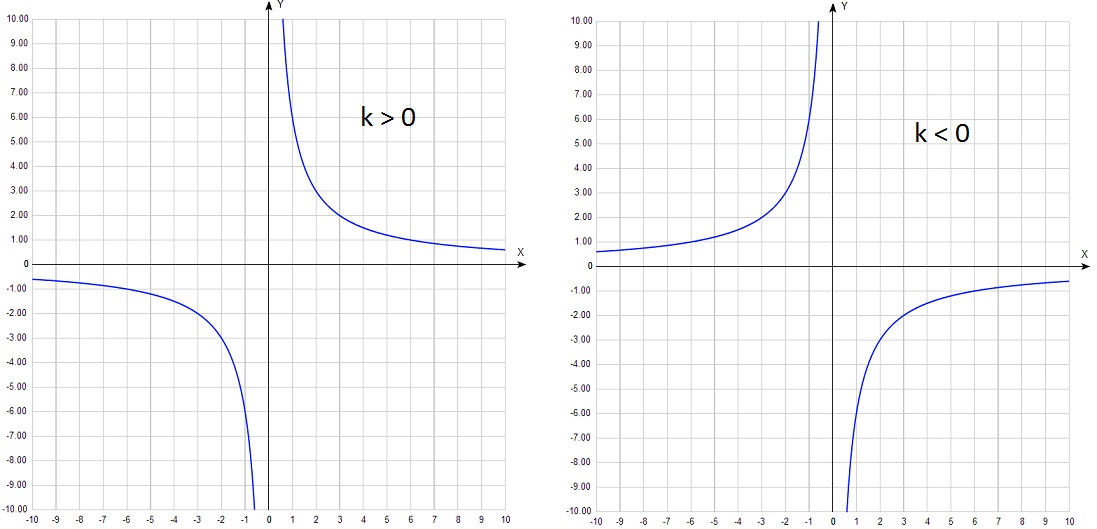
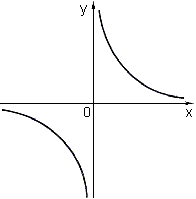
![Гипербола (обратная пропорциональность) [wiki.eduVdom.com]](https://wiki.eduvdom.com/_media/subjects/mathematics/03-gip-y-kx_k_0.png?w\u003d500\u0026tok\u003d48c86c)
Заключение
Гипербола в физике является важной кривой, которая возникает при изучении различных физических явлений. Она определяется как множество точек на плоскости, для которых модуль разности расстояний от двух фокусов постоянен. Гипербола имеет свои особенности и применение в различных областях физики, таких как оптика, гравитационная физика и электрические цепи.