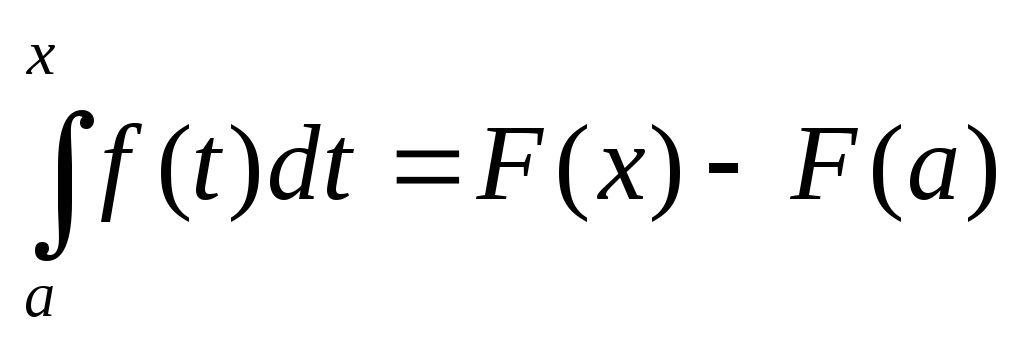Формула Ньютона-Лейбница является основной формулой интегрального исчисления. Она применяется для вычисления точного значения определенного интеграла. В большинстве прикладных задач вычисление точного значения определенного интеграла не является целесообразным или даже возможным. Однако, в некоторых случаях можно вычислить определенный интеграл точно с помощью формулы Ньютона-Лейбница. Узнайте больше об использовании формулы Ньютона-Лейбница в вычислениях определенных интегралов на NOCFN.
Где используется формула Ньютона-Лейбница?
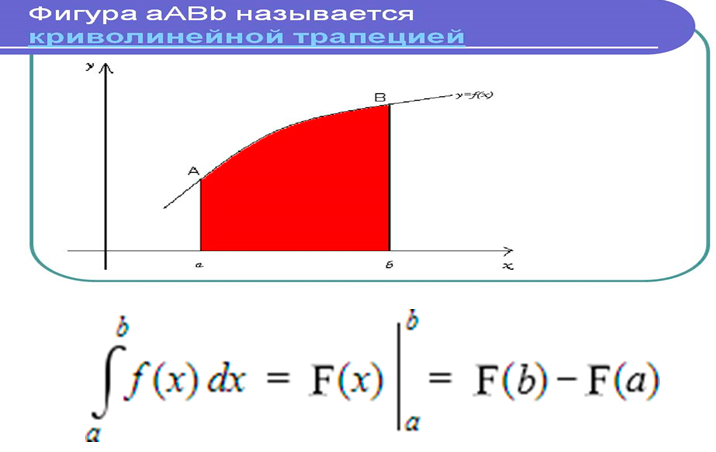
Формула Ньютона-Лейбница является основной формулой интегрального исчисления. Она применяется для вычисления точного значения определенного интеграла. В большинстве прикладных задач вычисление точного значения определенного интеграла не является целесообразным или даже возможным. Однако, в некоторых случаях можно вычислить определенный интеграл точно с помощью формулы Ньютона-Лейбница.
Доказательство
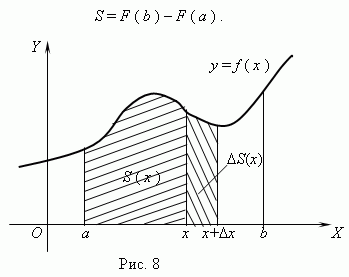
Пусть на отрезке [a, b] задана интегрируемая функция f. Зададим произвольное значение x ∈ [a, b] и определим новую функцию F(x) = ∫axf(t) dt. Она определена для всех значений x ∈ [a, b], потому что если существует интеграл от f на [a, b], то существует также интеграл от f на [a, x], где a ≤ x ≤ b. Напомним, что по определению F(a) = ∫aaf(t) dt = 0.
Заметим, что F(b) = ∫abf(t) dt.
Использование формулы Ньютона-Лейбница в вычислениях
В большинстве случаев формула Ньютона-Лейбница применяется для вычисления определенного интеграла с требуемой точностью. Часто для нахождения приближенного значения определенного интеграла используются численные методы, такие как метод Симпсона, метод трапеций или метод прямоугольников. Однако, если известна первообразная функции f(x), то можно точно вычислить определенный интеграл с помощью формулы Ньютона-Лейбница.
Примеры использования формулы Ньютона-Лейбница
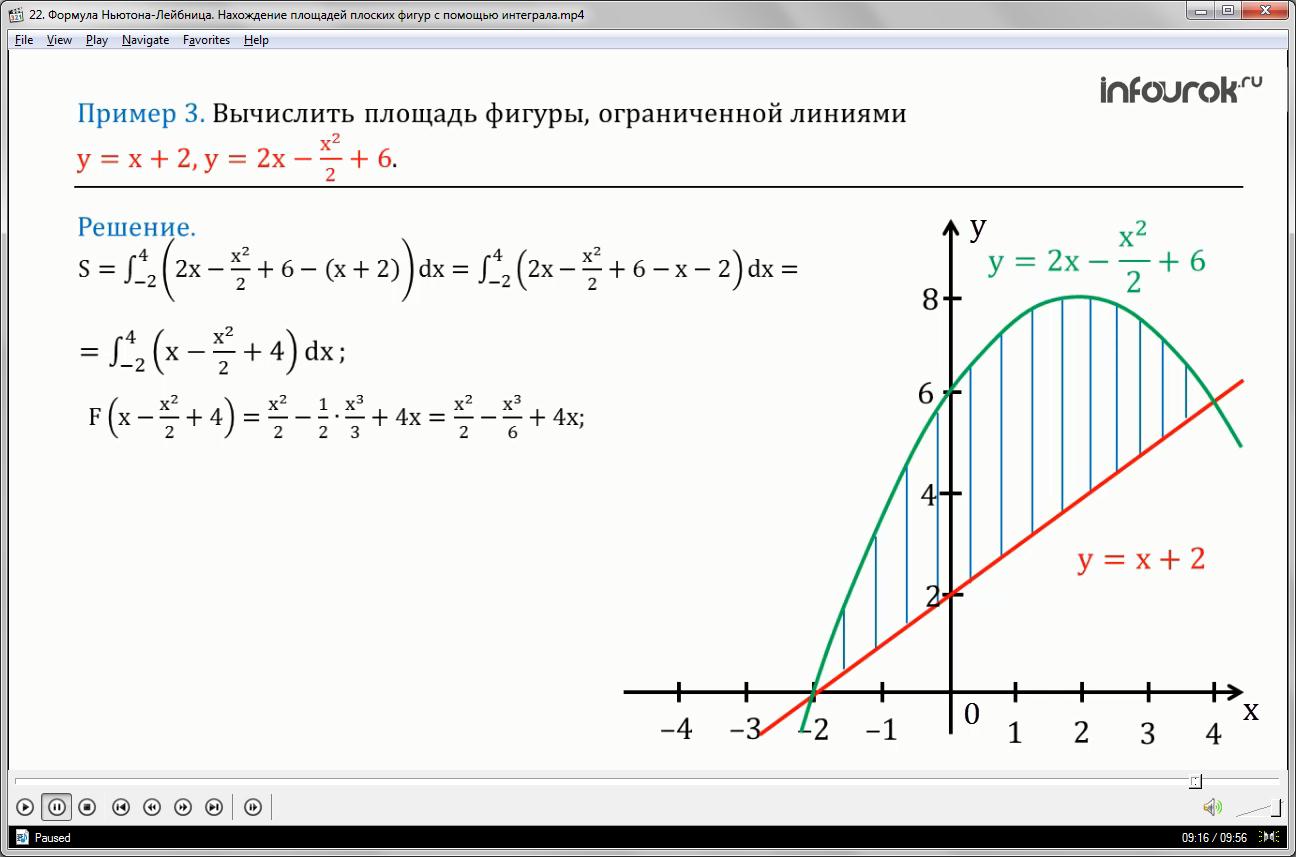
Рассмотрим несколько примеров применения формулы Ньютона-Лейбница для вычисления определенных интегралов.
| Пример | Интеграл | Решение |
|---|---|---|
| 1 | ∫01x2 dx | Пусть F(x) = (1/3)x3. Тогда F(1) - F(0) = (1/3) - 0 = 1/3. |
| 2 | ∫12(2x + 1) dx | Пусть F(x) = x2 + x. Тогда F(2) - F(1) = (22 + 2) - (12 + 1) = 6 - 2 = 4. |
В этих примерах формула Ньютона-Лейбница применяется для вычисления определенных интегралов с известными первообразными функциями.
Замена переменной и интегрирование по частям
В некоторых случаях для упрощения вычислений определенных интегралов можно использовать замену переменной или интегрирование по частям. Эти методы также основаны на формуле Ньютона-Лейбница и позволяют свести сложные интегралы к более простым. Например, при замене переменной можно привести интеграл к виду, в котором известна первообразная функция. При интегрировании по частям можно преобразовать интеграл, выделив часть функции для дифференцирования и другую часть для интегрирования.

Заключение
Формула Ньютона-Лейбница является важным инструментом в вычислениях определенных интегралов. Она позволяет точно вычислять значения определенных интегралов, если известна первообразная функция. Формула Ньютона-Лейбница также используется в методах замены переменной и интегрирования по частям для упрощения вычислений. Все эти методы основаны на основной формуле интегрального исчисления - формуле Ньютона-Лейбница.