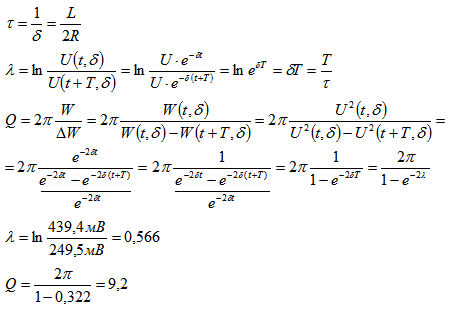Чем определяется резонансная частота контура?

Колебательный контур является типичным представителем резонансных колебательных систем, используемых в различных областях физики. Изучение параметров и свойств колебательного контура помогает понять основы резонансных систем.

Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в различных разделах физики. Он используется в механике, электродинамике, оптике и других областях. Изучение параметров и свойств колебательного контура помогает понять основы резонансных колебательных систем.

Основные понятия

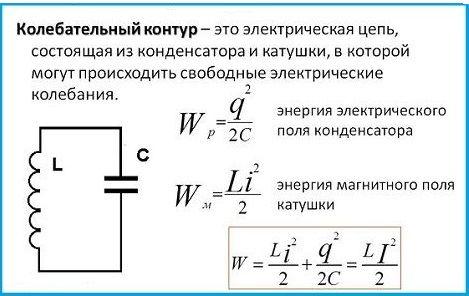
В теории колебаний выделяются два класса явлений: линейные и нелинейные. Линейные системы имеют параметры, которые не зависят от амплитуды колебаний. Для электрических колебательных контуров это означает, что индуктивность L, емкость C и сопротивление R не зависят от амплитуды токов и напряжений.

Резонансные системы обладают двумя важными свойствами. Они характеризуются резонансной частотой и добротностью. Резонансная частота контура определяется формулой Томсона, которая зависит от индуктивности и ёмкости контура.

Что такое резонансная частота контура?

Резонансная частота контура определяется так называемой формулой Томсона:

ω₀ = 1/√(LC),

где ω₀ - резонансная частота, L - индуктивность катушки, C - ёмкость конденсатора.

Эта формула показывает, что резонансная частота контура определяется произведением индуктивности и ёмкости. На одной и той же частоте может работать множество контуров с разными значениями L и C, но с одинаковым произведением LC.

Добротность контура

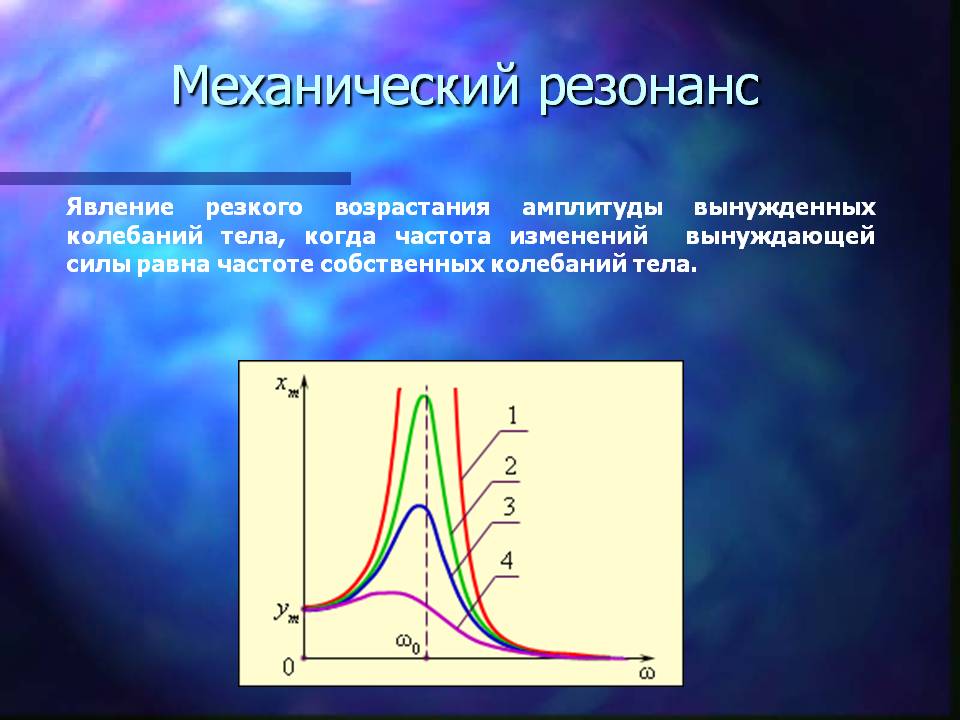
Добротность контура (Q-фактор) характеризует отношение мощности энергии собственного колебания к мощности потерь за период. Добротность контура можно рассчитать по следующей формуле:

Q = ω₀ / Δω,

где Δω - ширина резонансной кривой, определяющая разницу между частотами, на которых амплитуда колебаний уменьшается в √2 раза.

Для последовательного контура добротность растёт с увеличением индуктивности, а для параллельного контура добротность равна:

Q = 1 / (RC),

где R - сопротивление контура, C - ёмкость конденсатора.

Малые потери, то есть высокая добротность, означают, что сопротивление R в последовательном контуре мало, а в параллельном контуре велико.

Применение резонансных контуров

Резонансные контуры находят практическое применение в усилителях, радиоприёмниках и других устройствах автоматики. Они используются как полосовые и режекторные фильтры, обеспечивая стабильность частоты сигнала. Кроме того, резонансные контуры используются в системах поддержания постоянства частоты, например, на самолётах.

Изучение параметров и свойств колебательного контура помогает понять принципы работы резонансных колебательных систем и их практическое применение.

Что нам скажет Википедия?

Резонансная частота контура определяется так называемой формулой Томсона:

где L — индуктивность катушки, C — ёмкость конденсатора. Эта формула показывает, что на одной и той же частоте может работать множество контуров с разными значениями L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C не является произвольным, так как обуславливается требуемым значением добротности контура.

Для последовательного контура добротность растёт с увеличением L, а для параллельного контура добротность равна:

где Re — эквивалентное сопротивление, RL+C — сумма активных сопротивлений в цепи катушки и цепи конденсатора. Малые потери, то есть высокая добротность, означают, что Re в последовательном контуре мало, а в параллельном — велико.

Резонансные контуры находят практическое применение в усилителях, радиоприёмниках и других устройствах автоматики. Они используются как полосовые и режекторные фильтры, обеспечивая стабильность частоты сигнала. Например, на самолётах Ил-62М, Ил-76 и Ту-154М установлены блоки регулирования частоты, в которых применяются резонансные контуры для поддержания постоянства частоты напряжения генератора при изменении оборотов двигателя.