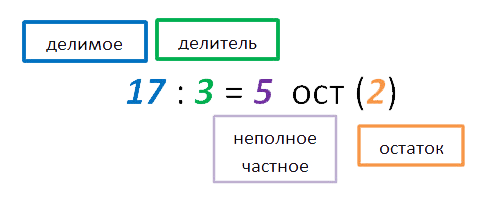Узнайте, как вычислить остаток от деления и выполнить проверку правильности решения. Подробный разбор алгоритмов деления с остатком целых чисел. Онлайн-курсы математики для детей.
Cодержание
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Эту формулу можно использовать для проверки деления с остатком.
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно.

Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
См. также
Алгоритм деления положительного числа на целое отрицательное (с остатком)
Разделить 17 на −5 с остатком.
Как решаем:
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного
Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом.
Пусть a и b — целые числа, причём b ≠ 0. Деление с остатком a («делимого») на b («делитель») означает нахождение таких целых чисел q и r, что выполняется равенство:
a = b · q + r
Таким образом, результатами деления с остатком являются два целых числа: q называется неполным частным от деления, а r — остатком от деления. На остаток налагается дополнительное условие: 0 ≤ r |b|, то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения a = b · q + r при заданных выше условиях. Если остаток равен нулю, говорят, что a нацело делится на b.
Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последнего термина стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).

Что нам скажет Википедия?
Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом. Пусть a и b — целые числа, причём b ≠ 0. Деление с остатком a («делимого») на b («делитель») означает нахождение таких целых чисел q и r, что выполняется равенство:
Таким образом, результатами деления с остатком являются два целых числа: q называется неполным частным от деления, а r — остатком от деления. На остаток налагается дополнительное условие: 0 ≤ r < |b|, то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения a = b · q + r при заданных выше условиях. Если остаток равен нулю, говорят, что a нацело делится на b.
Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последнего термина стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).