Узнайте признаки и условия, по которым можно понять, делится ли число на 10 без остатка. Проверка четности, сумма цифр и наличие нуля в конце числа - ключевые признаки делимости на 10. Узнайте все подробности в этой статье.
Cодержание
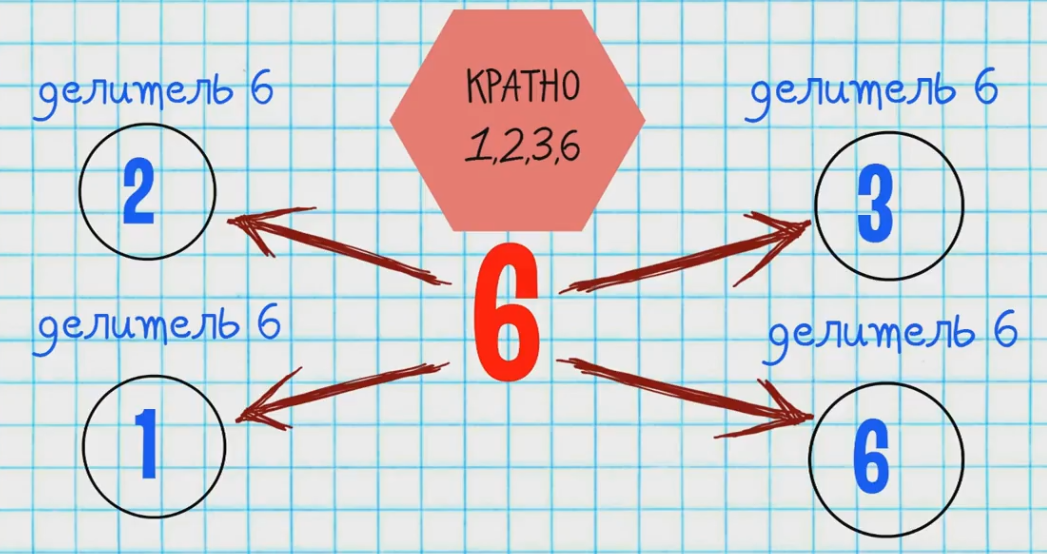
Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3. Другими словами, чтобы число делилось на 6, оно должно быть четным, а сумма его цифр должна быть кратной 3.

Примеры:
Рассмотрим несколько примеров:
| Число | Делится на 6? | Признак делимости на 2 | Признак делимости на 3 |
|---|---|---|---|
| 462 | Да | Да (последняя цифра 2 делится на 2) | Да (сумма цифр числа делится на 3: 4+6+2=12, 12:3=4) |
| 3456 | Да | Да (последняя цифра 6 делится на 2) | Да (сумма цифр числа делится на 3: 3+4+5+6=18, 18:3=6) |
| 24642 | Да | Да (последняя цифра 2 делится на 2) | Да (сумма цифр числа делится на 3: 2+4+6+4+2=18, 18:3=6) |
| 861 | Нет | Нет (не делится на 2) | Нет (не делится на 3) |
| 3458 | Нет | Нет (не делится на 2) | Нет (не делится на 3) |
| 34681 | Нет | Нет (не делится на 2) | Нет (не делится на 3) |
Если последняя цифра числа отлична от нуля, то это число не делится без остатка на 10. Остаток в этом случае равен последней цифре числа.
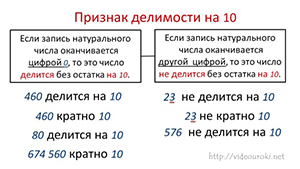
Вывод: если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10.
Число 10 – это произведение 2*5. Число 10 делится без остатка на 2 и на 5. Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка на 5 и на 2.
Примеры:
Рассмотрим несколько примеров:
| Число | Делится на 10? | Признак делимости на 5 | Признак делимости на 2 |
|---|---|---|---|
| 60 | Да | Да (последняя цифра 0 делится на 5) | Да (последняя цифра 0 делится на 2) |
| 870 | Нет | Да (последняя цифра 0 делится на 5) | Нет (последняя цифра 0 делится на 2) |
| 875 | Да | Да (последняя цифра 5 делится на 5) | Нет (последняя цифра 5 не делится на 2) |
Числа, делящиеся без остатка на 2, называют четными, а числа, которые при делении на 2 дают остаток 1, называют нечетными.
Вывод: если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно.
Продолжаем разговор о признаках делимости. В этом материале мы изучим, по каким признакам можно определить делимость числа на 1000, 100 и т.д.
См. также
Формулировка признака делимости на 10, 100 и т.д. с примерами:
Признак делимости числа на 10, 100 и т.д. основан на количестве нулей в конце числа.
Формулировки признаков:
- Число делится на 10, если оно оканчивается нулем.
- Число делится на 100, если оно оканчивается двумя нулями.
- Число делится на 1000, если оно оканчивается тремя нулями.
- И так далее, в зависимости от количества нулей в конце числа.
Например:
- 200 делится на 10 (оканчивается нулем).
- 4 000 делится на 100 (оканчивается двумя нулями).
- 500 000 делится на 1000 (оканчивается тремя нулями).
Отметим, что эти признаки нельзя применять к числу 0, так как 0 можно разделить на любое целое число без остатка.
Эти признаки легко применять в решении задач, так как подсчитать количество нулей в числе несложно.
Доказательство признаков делимости на 10, 100, 1000 и т.д.:
Для доказательства признаков делимости на 10, 100, 1000 и т.д. можно использовать знания о умножении натуральных чисел на 10, 100, 1000 и т.д., а также свойства делимости.
Для примера рассмотрим доказательство признака делимости на 10.
Доказательство необходимости условия:
Пусть некое число a можно разделить на 10 без остатка. Докажем, что в конце этого числа стоит 0.
Математически это можно записать так:
a = 10 * b, где b - целое число.
Так как 10 = 2 * 5, то a можно также представить как a = 2 * (5 * b).
Заметим, что число 5 * b - это целое число, так как умножение на 5 не меняет четность числа.
Таким образом, получаем, что a = 2 * целое число, что означает, что a четно.
Доказательство достаточности условия:
Пусть число a оканчивается нулем. Докажем, что оно делится на 10 без остатка.
Математически это можно записать так:
a = 10 * b, где b - целое число.
Таким образом, мы показали, что признак делимости на 10 является необходимым и достаточным условием.
Аналогично можно доказать признаки делимости на 100, 1000 и т.д., используя знания о умножении и свойствах делимости.
Таким образом, признаки делимости на 10, 100, 1000 и т.д. являются удобным инструментом для определения делимости чисел без необходимости выполнения деления.
Важно помнить, что эти признаки применимы только к натуральным числам, и число 0 не подчиняется этим правилам, так как 0 можно разделить на любое целое число без остатка.

Что нам скажет Википедия?
Математически этот признак равноостаточности может быть сформулирован следующим образом. Пусть надо выяснить остаток от деления на 10 натурального числа A, представленного в виде
A = anan-1...a1a0
Тогда остатком от деления A на 10 будет a0. Функция, описывающая этот признак равноостаточности будет выглядеть как
f(x) = x mod 10
Легко доказать, что эта функция удовлетворяет всем перечисленным выше требованиям. Причём последовательность, построенная с её помощью, будет содержать всего один или два члена.
Также легко видеть, что такой признак ориентирован именно на десятичное представление числа A — так, например, если применять его на компьютере, использующем двоичную запись числа, то чтобы выяснить a, программе пришлось бы сначала поделить A на 10.