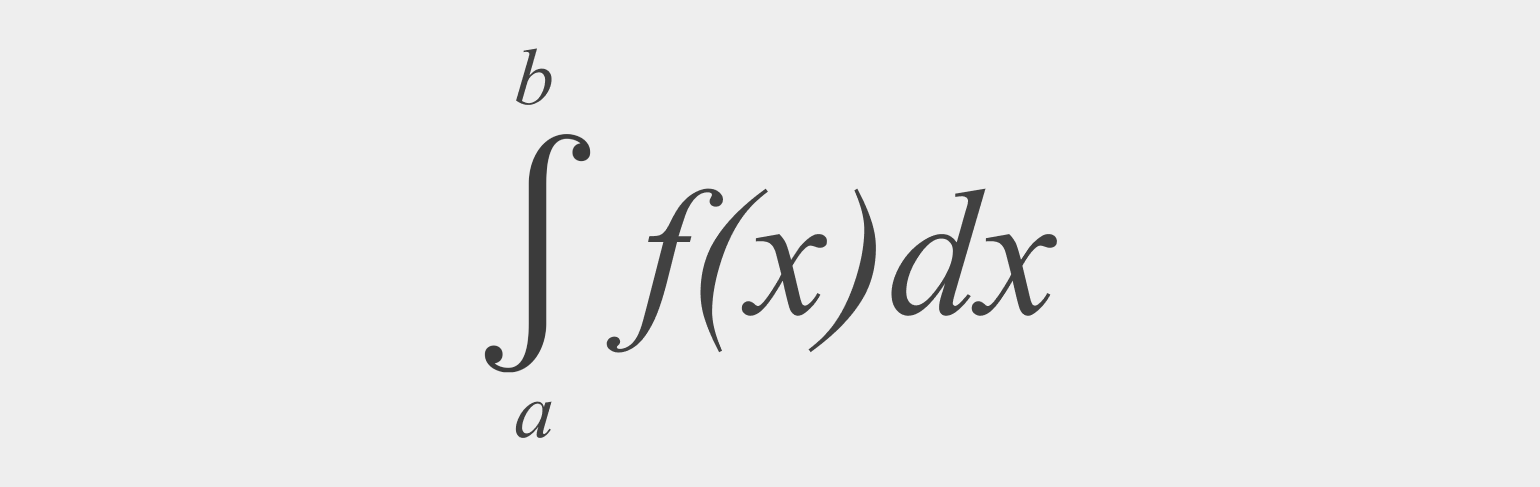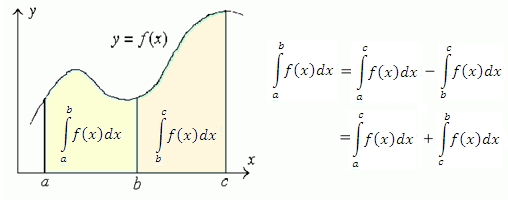Как обозначают определенный интеграл?

Узнайте, как обозначают определенный интеграл и его определение в статье на NOCFN.

Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм). Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции.

Определение

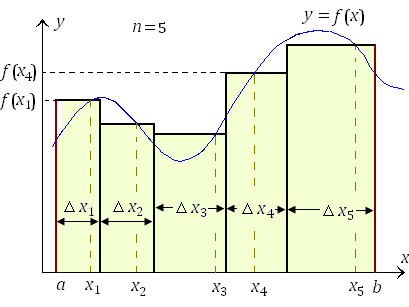
Пусть функция f(x) определена на отрезке [a; b]. Разобьём отрезок [a; b] на части несколькими произвольными точками: a = x₀ x₁ x₂ ... x_n = b. Тогда говорят, что произведено разбиение R отрезка [a; b].

Далее, для каждого i от 0 до n-1 выберем произвольную точку ξ_i ∈ [x_i; x_i+1].

Определённым интегралом от функции f(x) на отрезке [a; b] называется предел интегральных сумм при стремлении ранга разбиения к нулю, если он существует независимо от разбиения R и выбора точек ξ_i, то есть:

Если существует указанный предел, то функция f(x) называется интегрируемой на [a; b] по Риману.

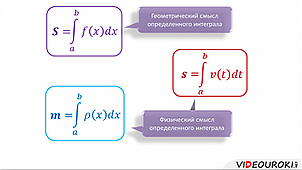
Обозначения

Определённый интеграл от неотрицательной функции ∫_a^b f(x) dx численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Что нам скажет Википедия?

Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм). Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции.

Определённым интегралом от функции f(x) на отрезке [a; b] называется предел интегральных сумм при стремлении ранга разбиения к нулю, если он существует независимо от разбиения R и выбора точек ξ_i, то есть

Если существует указанный предел, то функция f(x) называется интегрируемой на [a; b] по Риману.

Обозначения

Определённый интеграл от неотрицательной функции ∫_a^b f(x) dx численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).