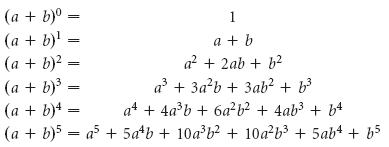Биномиальные коэффициенты - это числа, которые используются для подсчета количества способов выбрать набор элементов из заданного множества без учета порядка. Они являются коэффициентами в разложении бинома Ньютона и имеют широкие применения в комбинаторике и теории вероятностей. Узнайте историю, определение, способы вычисления и свойства биномиальных коэффициентов. Также узнайте о применении и обобщении, алгоритмах вычисления и заключении.
Cодержание
Биномиальные коэффициенты - это числа, которые используются для подсчета количества способов выбрать набор элементов из заданного множества без учета порядка. Они являются коэффициентами в разложении бинома Ньютона и имеют широкие применения в комбинаторике и теории вероятностей.

История и обозначения
Биномиальные коэффициенты были известны еще в древние времена. Они встречаются в индийских математических текстах, таких как "Чандамшастра Пингалы", написанного Халаюдхой в 10 веке. Однако формальное обозначение (n k) для биномиального коэффициента было введено Андреасом фон Эттингсхаузеном в 19 веке.
Определение и вычисление
Биномиальные коэффициенты (n k) определяются как количество способов выбрать k элементов из n-элементного множества. Имеются различные способы вычисления биномиальных коэффициентов:
- Аналитическая формула: (n k) = n! / (k!(n - k)!)
- Рекуррентная формула: (n k) = (n-1 k-1) + (n-1 k)
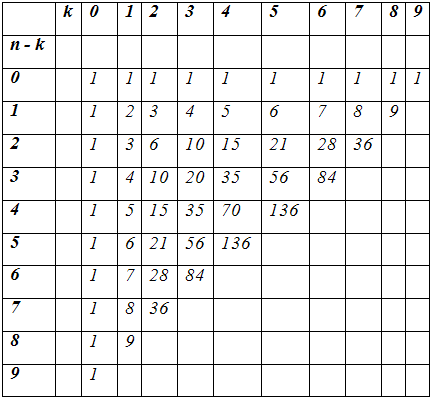
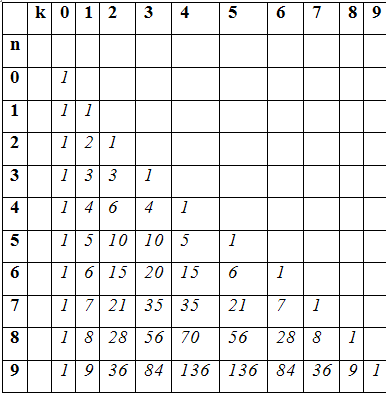
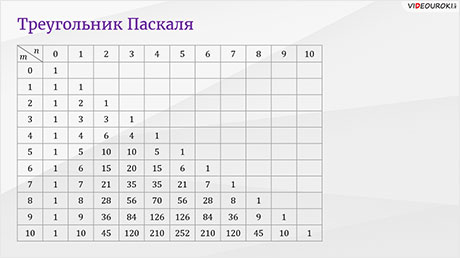
Также биномиальные коэффициенты можно вычислить с помощью треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих чисел.
См. также
Свойства биномиальных коэффициентов
Биномиальные коэффициенты обладают различными свойствами:
- Симметрия: (n k) = (n n-k)
- Делимость: (n k) делится на простое число p, если p является простым делителем n и не является делителем k
- Сумма по столбцам: сумма биномиальных коэффициентов в столбце треугольника Паскаля равна степени числа 2

Применение и обобщение
Биномиальные коэффициенты широко применяются в комбинаторике, теории вероятностей и других областях математики. Они также могут быть обобщены до мультиномиальных коэффициентов, которые используются для подсчета количества способов выбрать набор элементов из нескольких различных множеств.

Алгоритмы вычисления
Для вычисления биномиальных коэффициентов могут использоваться различные алгоритмы, такие как:
- Вычисление по аналитической формуле
- Использование рекурсии и мемоизации
- Использование треугольника Паскаля
Каждый из этих алгоритмов имеет свои преимущества и ограничения в зависимости от требуемой точности и эффективности вычислений.
См. также
Заключение
Биномиальные коэффициенты - это важный математический инструмент, который находит применение в различных областях. Они позволяют подсчитывать количество способов выбора элементов из заданного множества и имеют множество интересных свойств. Вычисление биномиальных коэффициентов может быть выполнено различными способами, включая аналитическую формулу, рекуррентную формулу и использование треугольника Паскаля.
Что нам скажет Википедия?
Биномиальный коэффициент — коэффициент перед членом разложения бинома Ньютона (1 + x)^n по степеням x. Коэффициент при x^k обозначается (n k) или C_n^k и читается «биномиальный коэффициент из n по k» (или «число сочетаний из n по k»). Биномиальные коэффициенты могут быть также определены для произвольных действительных показателей n. В случае произвольного действительного числа n биномиальные коэффициенты определяются как коэффициенты разложения выражения (1 + x)^n в бесконечный степенной ряд.
В комбинаторике биномиальный коэффициент (n k) для неотрицательных целых чисел n и k интерпретируется как количество сочетаний из n по k, то есть как количество всех (нестрогих) подмножеств (выборок) размера k в n-элементном множестве.
Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Вычисляя коэффициенты в разложении (1 + x)^n в степенной ряд, можно получить явные формулы для биномиальных коэффициентов (n k).
Для всех действительных чисел n и целых чисел k:
Формула Значение (n k) = n! / (k!(n - k)!) для 0 ≤ k ≤ n (n k) = 0 для k > n (n - 1 k - 1) + (n - 1 k) = (n k) для 0 < k < n Треугольник Паскаля позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих.
Свойства биномиальных коэффициентов также включают производящие функции, делимость, основные тождества, бином Ньютона и свертку Вандермонда.