Узнайте, что такое простые числа от 1 до 10 и как их определить. Простые числа имеют ровно два натуральных делителя и играют важную роль в математике и науке.
Cодержание
Просто́е число́ — натуральное число, имеющее ровно два различных натуральных делителя. Другими словами, натуральное число p является простым, если оно отлично от 1 и делится без остатка только на 1 и на само p.
Пример: число 2 простое (делится на 1 и на 2), а 4 не является простым, так как, помимо 1 и 4, делится на 2 — имеет три натуральных делителя.
Изучением свойств простых чисел занимается теория чисел, а основная теорема арифметики устанавливает в ней их центральную роль: любое целое число, превышающее 1, либо является простым, либо может быть выражено произведением простых чисел, причём такое представление однозначно с точностью до порядка сомножителей. Единицу не относят к простым числам, так как иначе указанное разложение становится неоднозначным.

Классификация натуральных чисел
Натуральные числа можно разделить на три класса:
- Единица (имеет один натуральный делитель).
- Простое число (имеет два натуральных делителя).
- Составное число (имеет более двух натуральных делителей).
Как простых, так и составных чисел бесконечно много.

Примеры простых и составных чисел
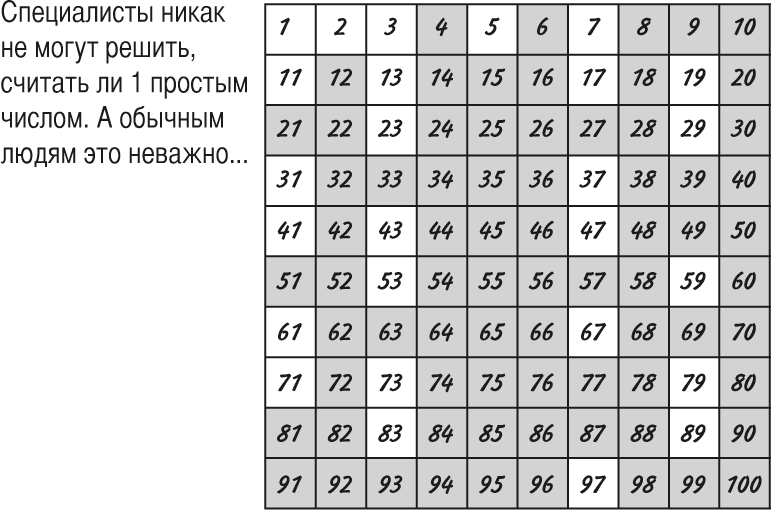
Простыми числами от 1 до 10 являются: 2, 3, 5, 7. Эти числа имеют только два натуральных делителя - 1 и само число.
Составными числами от 1 до 10 являются: 4, 6, 8, 9, 10. Эти числа имеют более двух натуральных делителей.
См. также
Алгоритмы проверки чисел на простоту
Существует несколько алгоритмов для проверки числа на простоту:
- Метод перебора делителей - примитивный и медленный алгоритм.
- Алгоритмы на основе тестов простоты, такие как тест Миллера-Рабина и тест Соловея-Штрассена, которые используются для проверки больших чисел.

Простые числа в математике и науке
Простые числа широко используются в математике и смежных науках. Они являются основой для многих алгоритмов информационных технологий, например, в асимметричных криптосистемах. Свойства простых чисел изучаются в теории чисел, которая является важной областью математики.

Самое большое и наименьшее простое число
Долгое время самым большим известным простым числом было простое число Мерсенна (M57885161), состоящее из 17 425 170 десятичных цифр. Однако, в 2018 году было обнаружено еще более большое простое число, равное 282 589 933−1, представленное в десятичной форме 24 862 048 цифр.
Наименьшим простым числом является число 2, которое также является единственным четным простым числом.
См. также
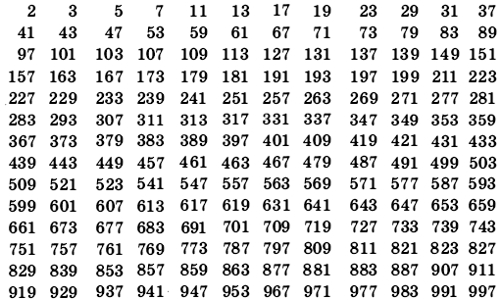
Список простых чисел от 1 до 100
Приведен список простых чисел от 1 до 100:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 |
| 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 |
| 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 |
Алгоритмы для определения простых чисел известны с древних времен. Например, греческий математик Эратосфен использовал метод удаления кратных чисел для нахождения простых чисел в заданном диапазоне.

Взаимно простые числа
Взаимно простые числа - это числа, у которых наибольший общий делитель равен единице. Например, числа 2, 11 и 419 являются взаимно простыми, так как у них нет общих делителей, кроме единицы.
Взаимно простыми могут быть как простые, так и составные числа. Например, числа 4 и 23 являются взаимно простыми, так как их наибольший общий делитель равен единице.
Таким образом, простые числа играют важную роль в математике и науке в целом. Их свойства изучаются в теории чисел, а алгоритмы для определения простых чисел используются в различных областях, включая информационные технологии и криптографию.

Что нам скажет Википедия?
Просто́е число́ — натуральное число, имеющее ровно два различных натуральных делителя. Другими словами, натуральное число p является простым, если оно отлично от 1 и делится без остатка только на 1 и на само p.
Пример: число 2 простое (делится на 1 и на 2), а 4 не является простым, так как, помимо 1 и 4, делится на 2 — имеет три натуральных делителя.
Изучением свойств простых чисел занимается теория чисел, а основная теорема арифметики устанавливает в ней их центральную роль: любое целое число, превышающее 1, либо является простым, либо может быть выражено произведением простых чисел, причём такое представление однозначно с точностью до порядка сомножителей. Единицу не относят к простым числам, так как иначе указанное разложение становится неоднозначным.
Натуральные числа можно разделить на три класса: единица (имеет один натуральный делитель), простое число (имеет два натуральных делителя), составное число (имеет более двух натуральных делителей). Как простых, так и составных чисел бесконечно много.