Гипербола представляет собой геометрическое место точек на плоскости, для которых модуль разности расстояний до двух заданных точек является постоянной и меньшей, чем расстояние между фокусами. Узнайте, сколько осей симметрии имеет гипербола и как она строится. Читайте статью на NOCFN.
Cодержание
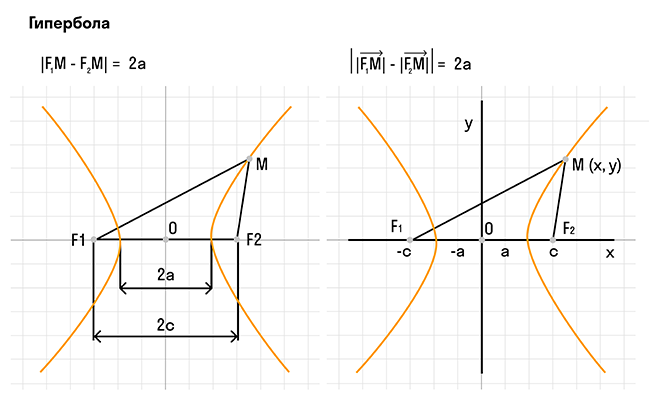
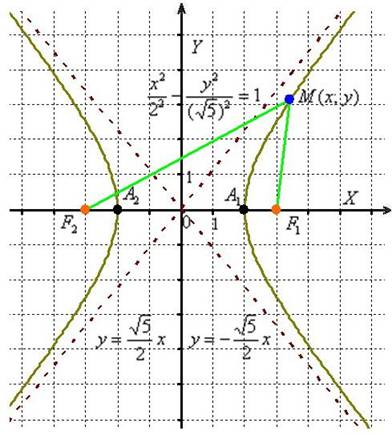
Гипербола представляет собой геометрическое место точек на плоскости, для которых модуль разности расстояний до двух заданных точек, называемых фокусами, является постоянной и меньшей, чем расстояние между фокусами.
Каноническое уравнение гиперболы
В алгебре каноническое уравнение гиперболы выглядит следующим образом:
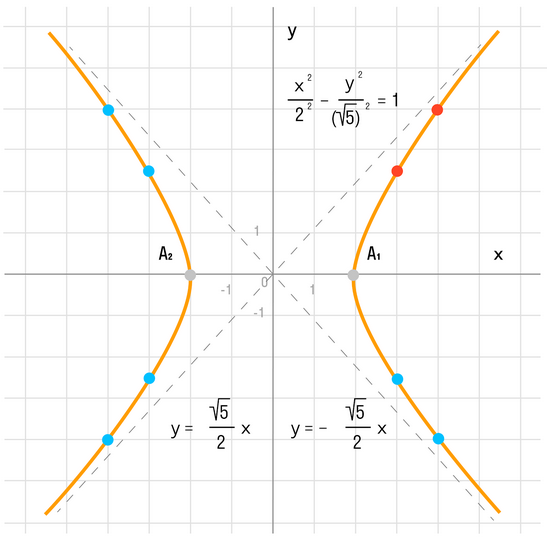
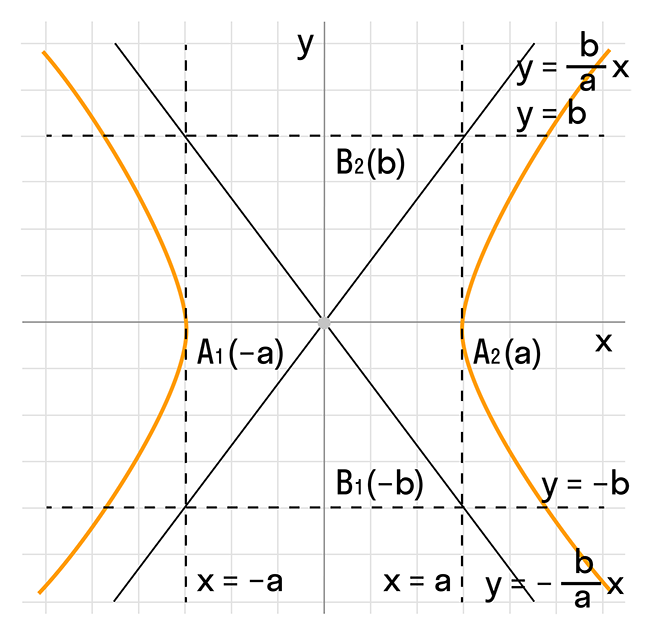
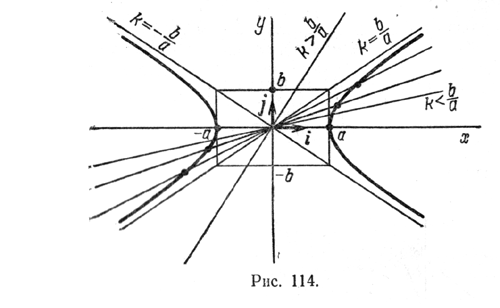
x2/a2 - y2/b2 = 1
где a и b - положительные действительные числа.
Форма гиперболы
Гипербола имеет следующую форму:
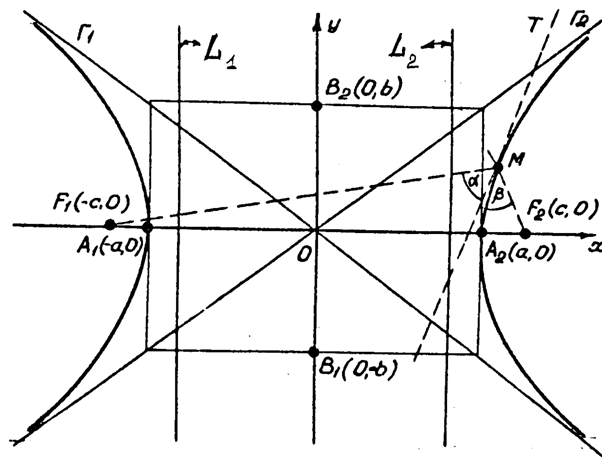
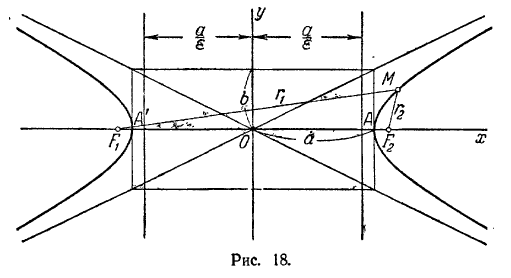
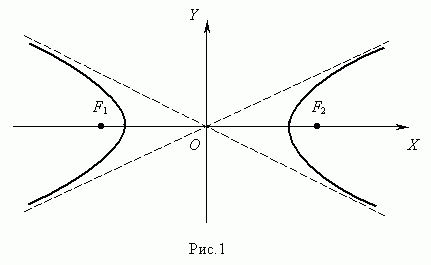
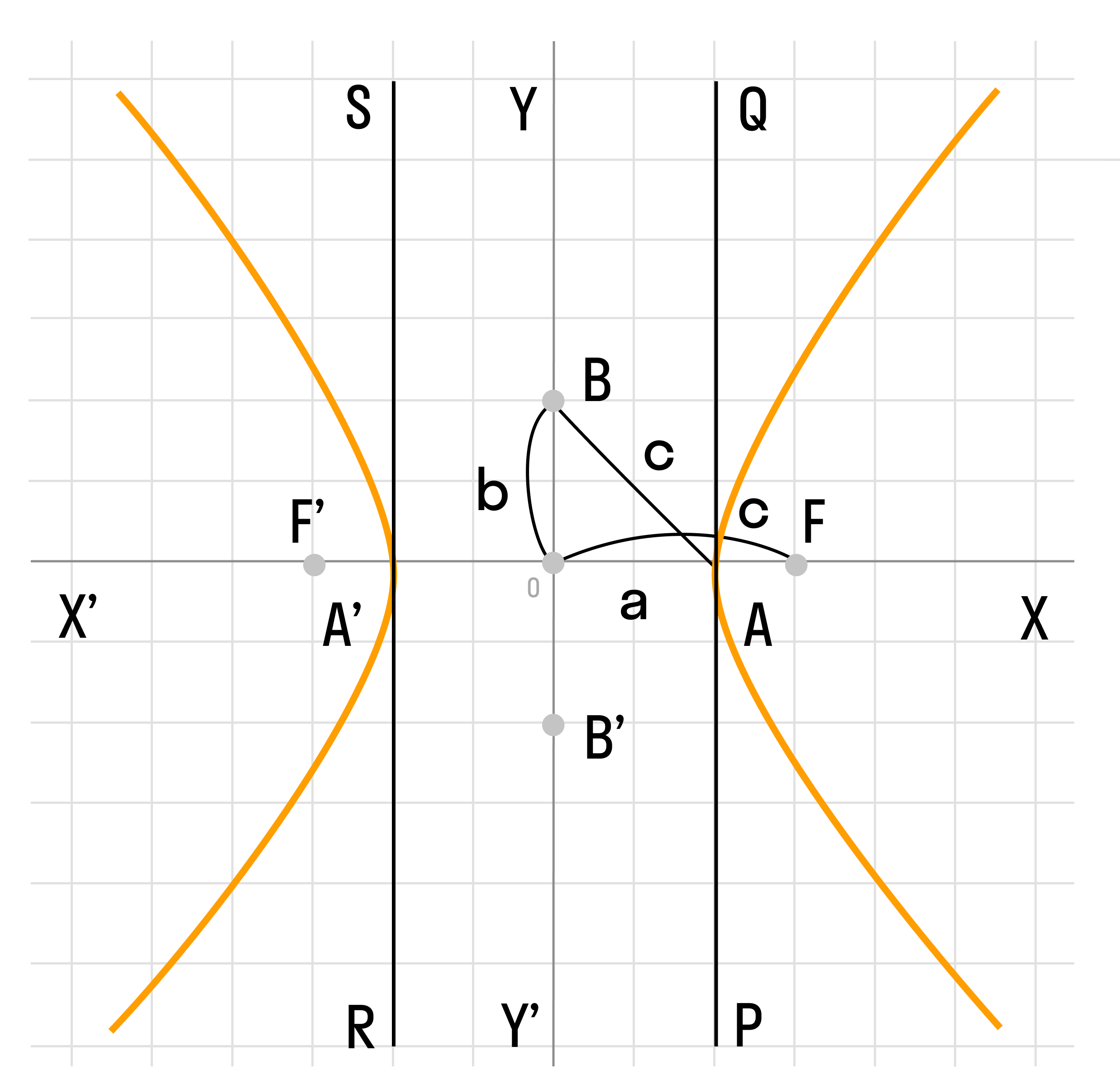
- Центр симметрии гиперболы находится в точке O, которая является серединой отрезка между фокусами F' и F.
- Прямая F'F пересекает гиперболу в двух точках A и A', которые являются вершинами гиперболы.
- Длина отрезка AA' равна 2a и называется действительной осью гиперболы.
- Прямая Y'Y, проведенная через точку O перпендикулярно прямой F'F, является осью симметрии гиперболы.
- Отрезок B'O=OB=b, отложенный на оси Y'Y, называется мнимой полуосью гиперболы.
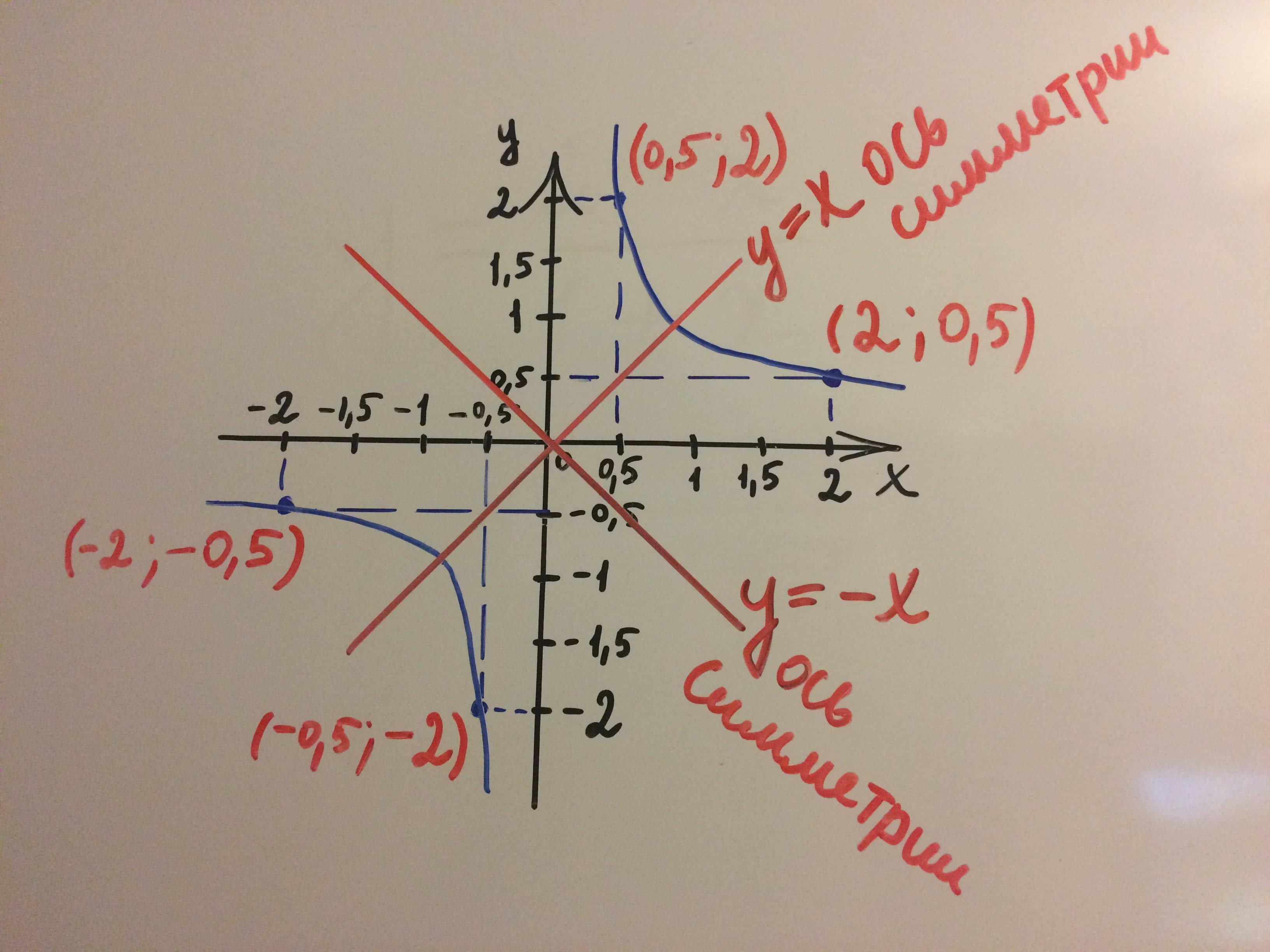
Симметрия гиперболы
Гипербола является симметричной относительно:
- Центра O
- Прямой F'F
- Прямой Y'Y
Количество осей симметрии
Гипербола имеет 3 оси симметрии: ось симметрии через центр O, ось симметрии через прямую F'F и ось симметрии через прямую Y'Y.