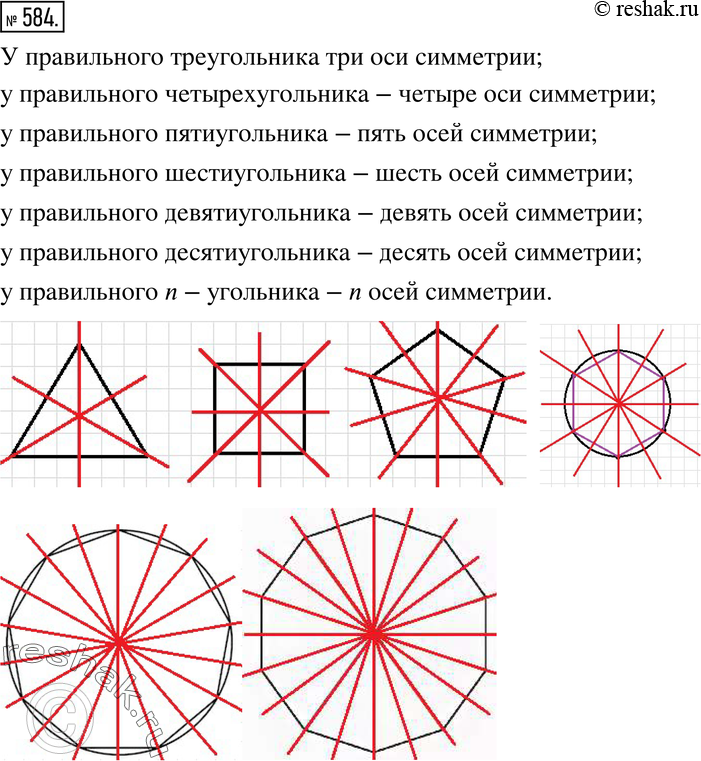
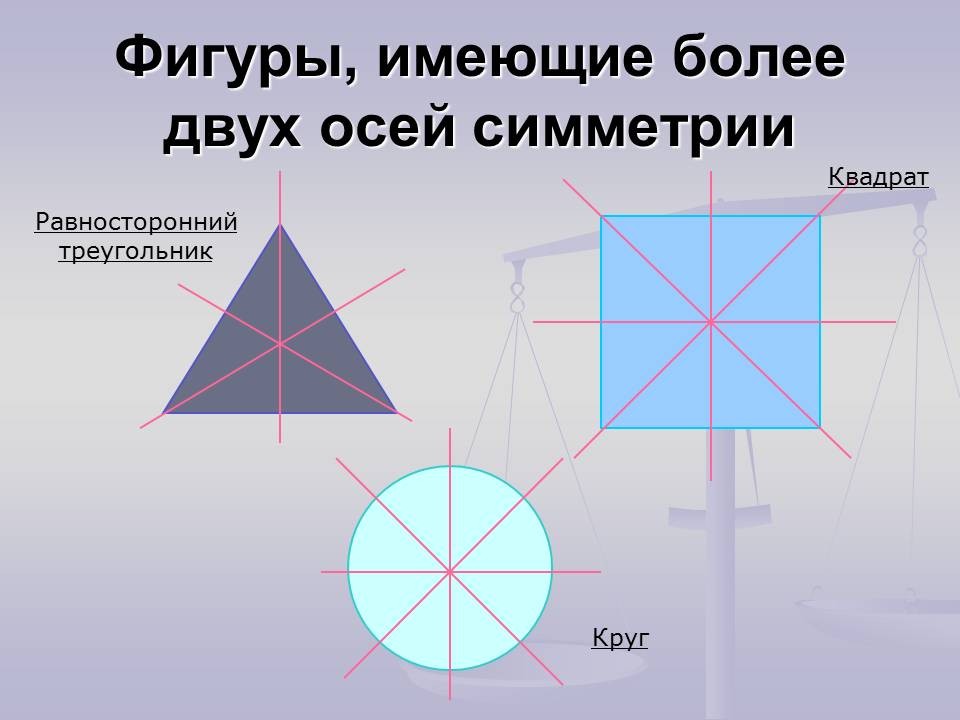
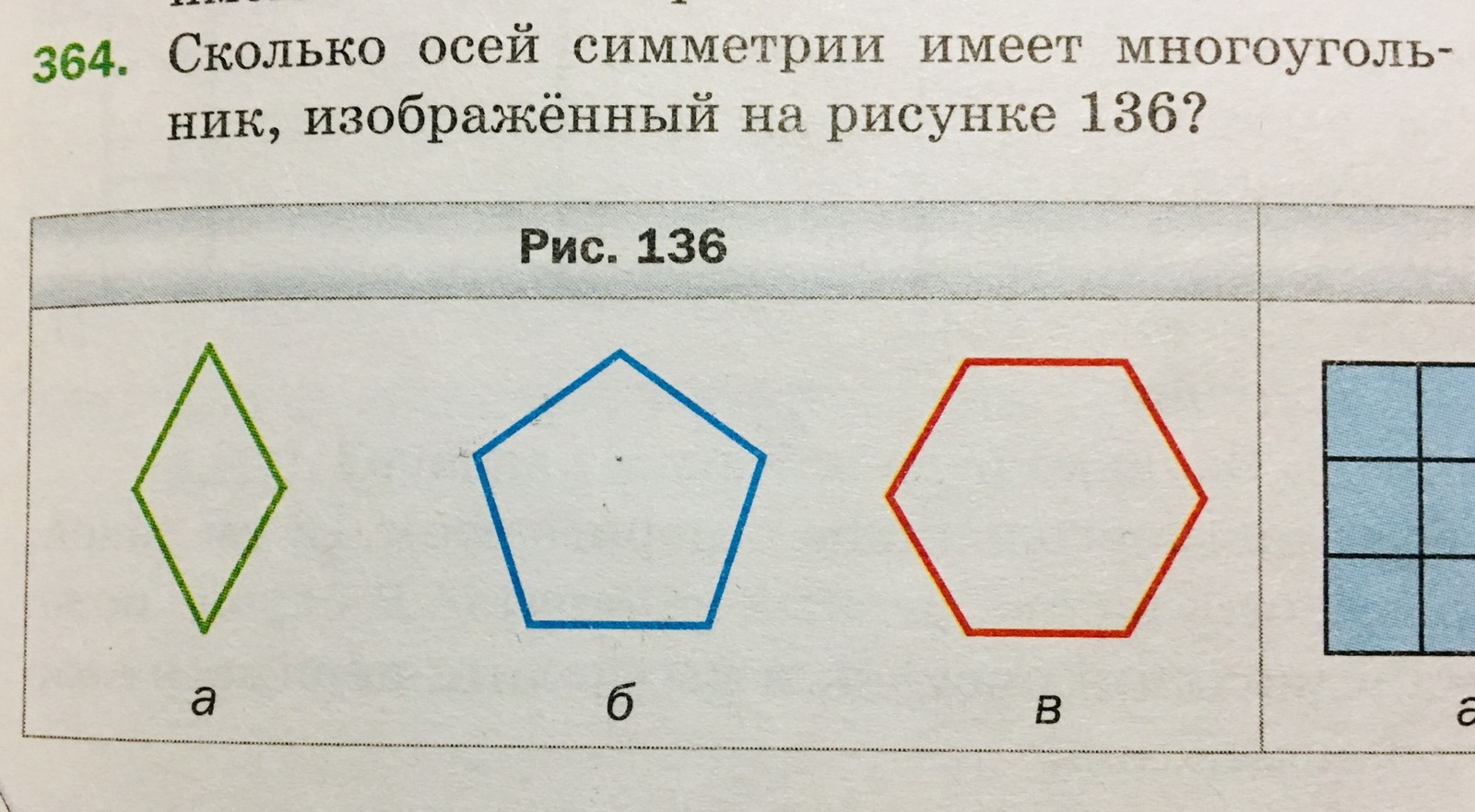
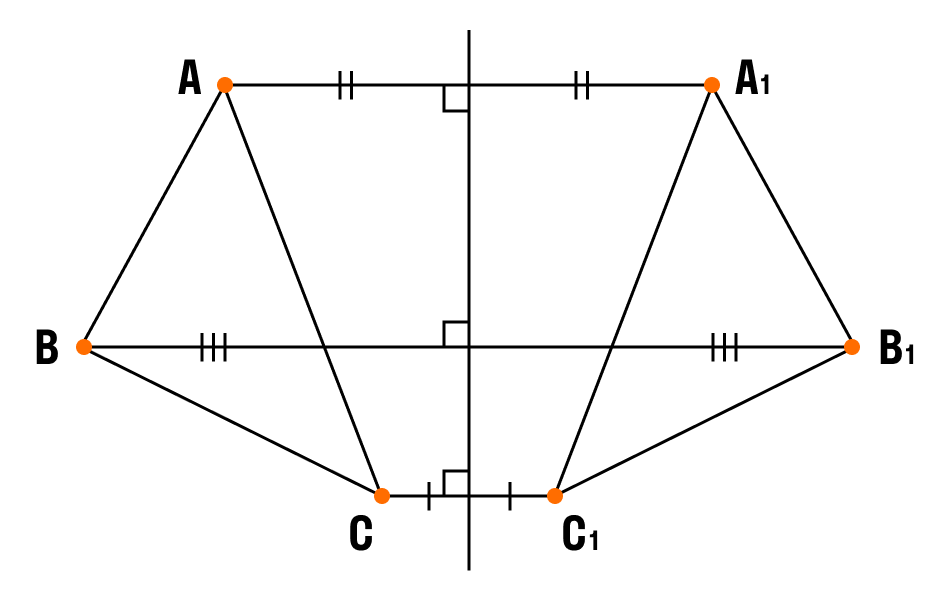
Симметрия - это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия. Узнайте больше о понятии оси симметрии и ее роли в создании симметричных фигур и структур.
Cодержание
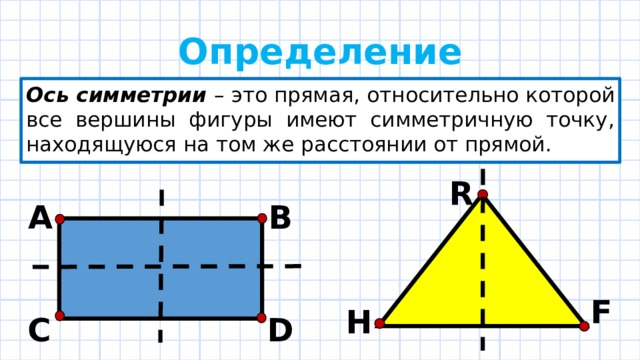
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
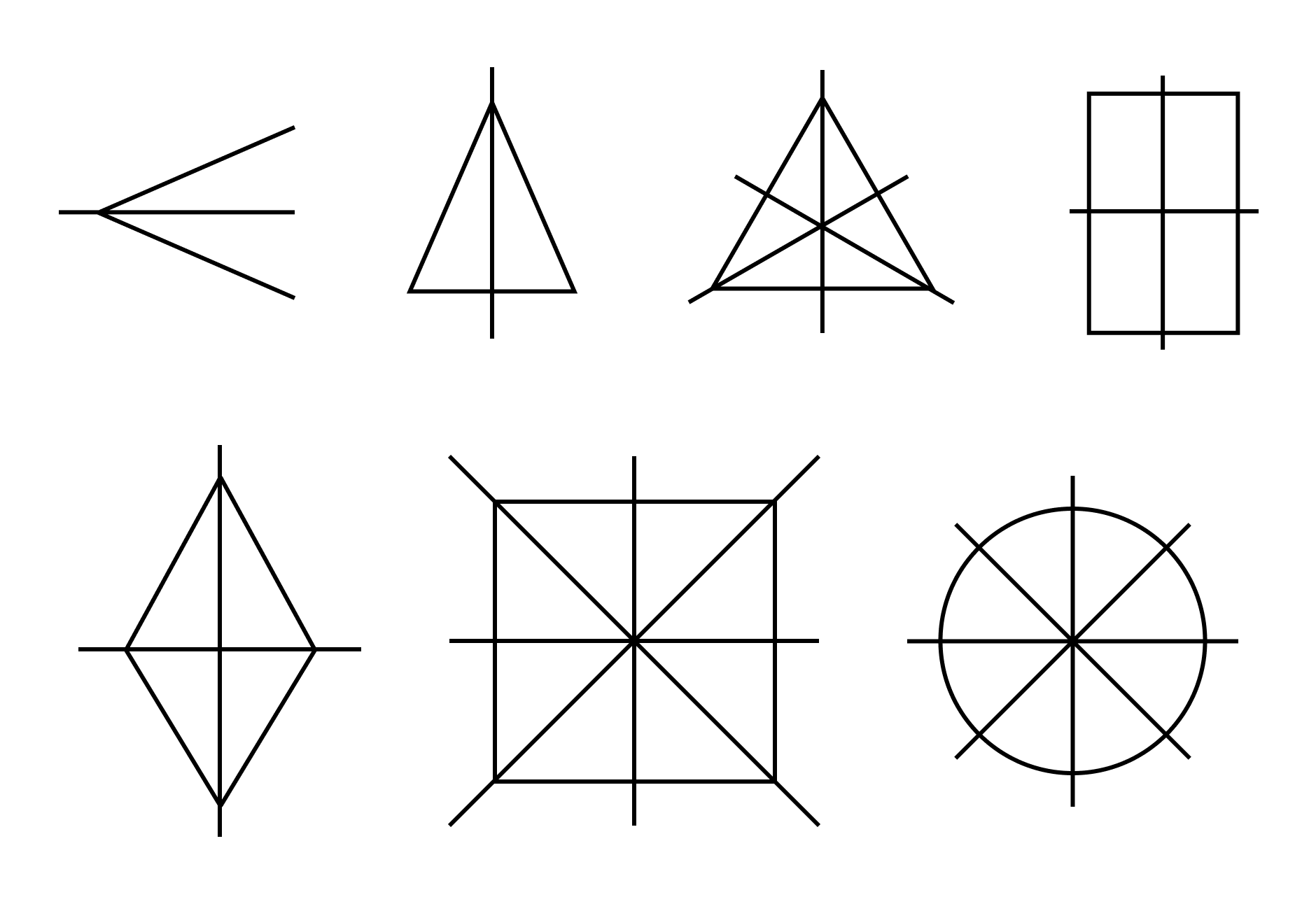
Ось симметрии
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
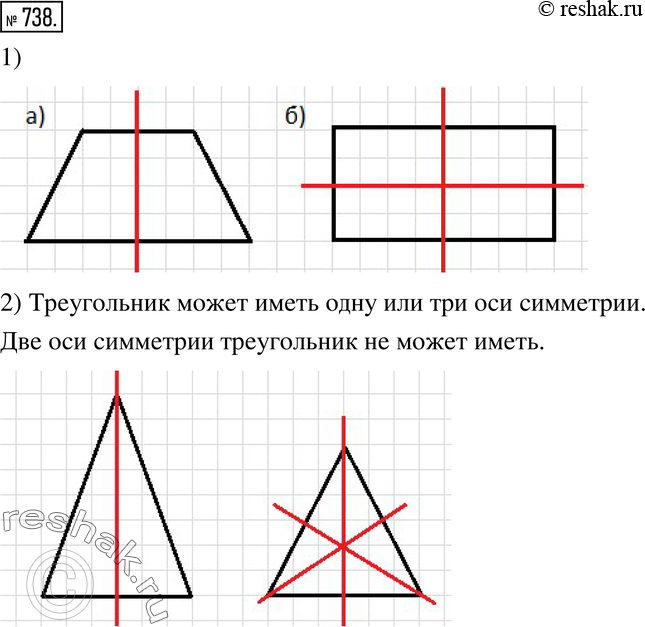
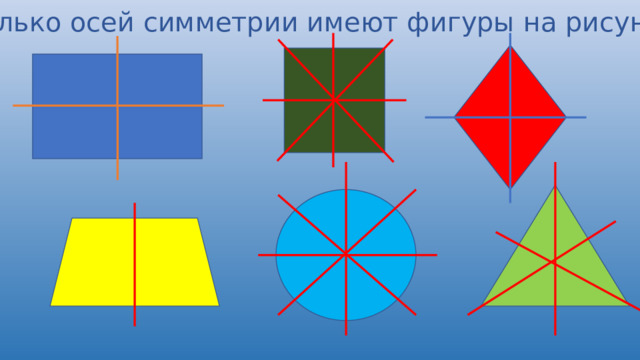
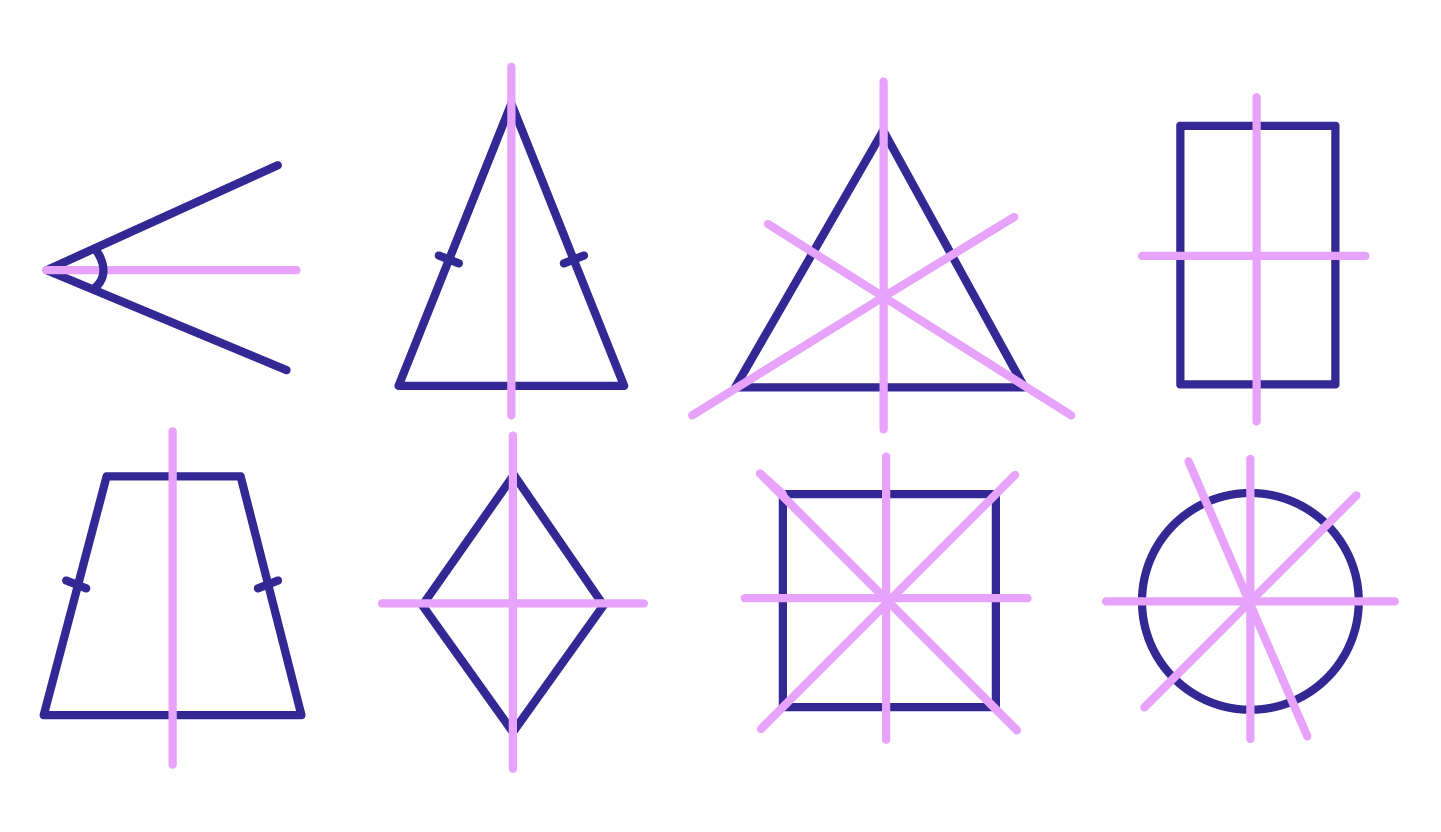
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Примеры построения фигур с осевой симметрией:
- Построить треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Построить треугольник, симметричный треугольнику ABC относительно прямой d.
- Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Центральная симметрия
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Примеры построения фигур с центральной симметрией:
- Построить фигуру, симметричную данной относительно точки O.
Симметрия играет важную роль в нашей жизни и может быть применена в различных областях, от архитектуры до биологии. Понимание осей симметрии позволяет нам анализировать и создавать симметричные фигуры и структуры.
Запомните, что симметрия придает объектам красоту и гармонию, искусство симметрии привлекает взгляд.
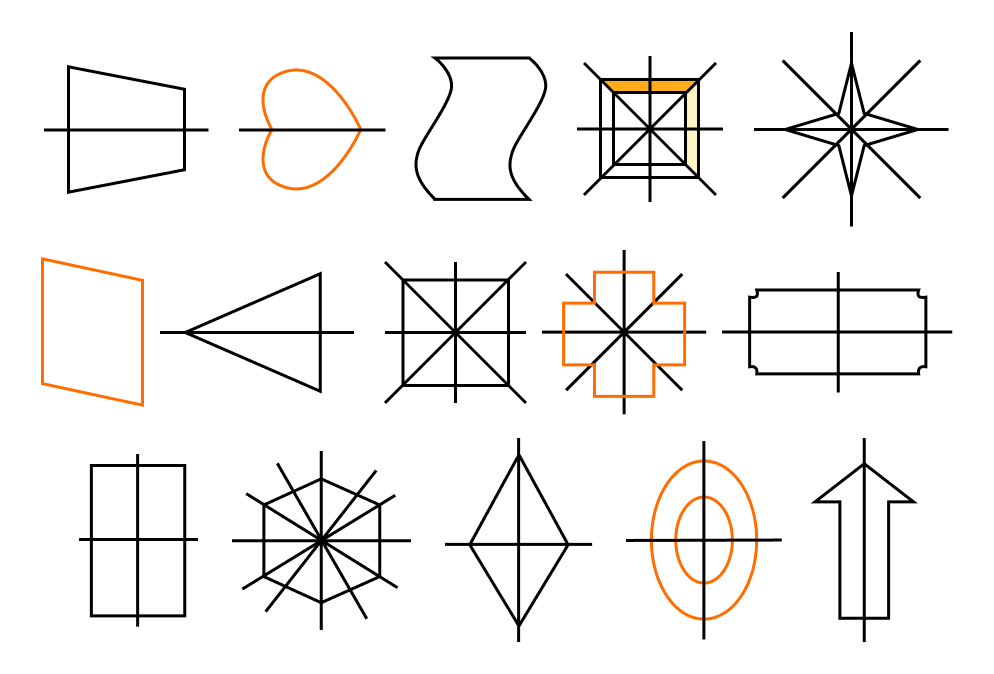
Что нам скажет Википедия?
Оси симметрии являются одним из элементов симметрии и характеризуют закономерное расположение подобных или одинаковых частей тела или форм живого организма относительно центра или оси симметрии. Обычно через центр симметрии проходят оси симметрии, а через ось симметрии проходят плоскости симметрии. Однако есть тела и фигуры, у которых при наличии центра симметрии нет ни осей, ни плоскостей симметрии, а при наличии оси симметрии отсутствуют плоскости симметрии.Среди элементов симметрии в биологии различают геометрические и биологические элементы. Геометрические элементы включают оси симметрии и плоскости симметрии. Биологические элементы включают сферическую, радиальную и билатеральную симметрию.
Радиальная симметрия, или лучевая симметрия, характеризуется формой симметрии, при которой тело или фигура совпадает само с собой при вращении объекта вокруг определённой точки или прямой. Эта точка обычно совпадает с центром симметрии объекта. Радиальной симметрией обладают такие геометрические объекты, как круг, шар, цилиндр или конус.
Билатеральная симметрия, или двусторонняя симметрия, характеризуется симметрией зеркального отражения. У билатерально симметричных объектов имеется одна плоскость симметрии, относительно которой две половины объекта зеркально симметричны. У животных билатеральная симметрия проявляется в схожести или полной идентичности левой и правой половин тела. Хотя всегда существуют случайные отклонения от симметрии, билатеральная симметрия является преобладающей у многоклеточных животных.