Гипербола является одним из геометрических мест точек на евклидовой плоскости. Узнайте об оптических свойствах гиперболы и ее определении.
Cодержание
Гипербола является одним из геометрических мест точек на евклидовой плоскости. Вместе с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Она может быть определена как множество точек, для которых абсолютное значение разности расстояний от точки M до двух фокусов F₁ и F₂ постоянно. Гипербола имеет свои оптические свойства, которые рассмотрим подробнее.

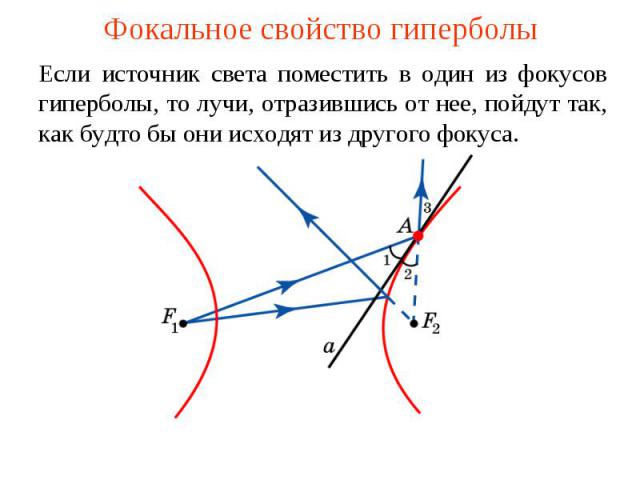
Оптические свойства гиперболы
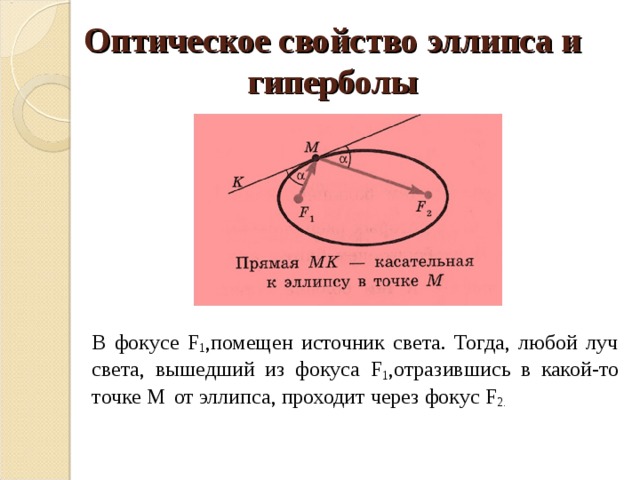
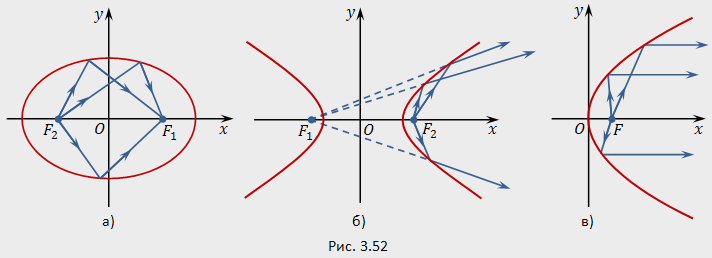
Одним из оптических свойств гиперболы является фокусировка световых лучей. Если поместить лампочку в одном из фокусов зеркального эллипса и проследить за выпущенными из неё лучами света, то мы увидим, что они после отражения от эллипса соберутся в другом фокусе. Это свойство гиперболы объясняется её геометрической природой.

Определение гиперболы
Гипербола может быть определена несколькими способами:
Коническое сечение
Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. При этом возникают также другие конические сечения, такие как парабола, эллипс и вырожденные случаи, например, пересекающиеся прямые и точка.
Через фокусы
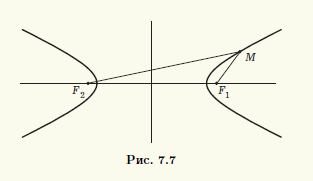
Гипербола может быть определена как геометрическое место точек, для которых абсолютная разность расстояний от них до двух заданных точек (фокусов) постоянна. Это определение позволяет явно выразить гиперболу с помощью уравнения и описывает её геометрическую природу.
Через директрису и фокус
Гипербола также может быть определена как геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы. Эксцентриситет гиперболы определяется постоянной величиной, которая должна быть больше единицы.
См. также
Форма гиперболы
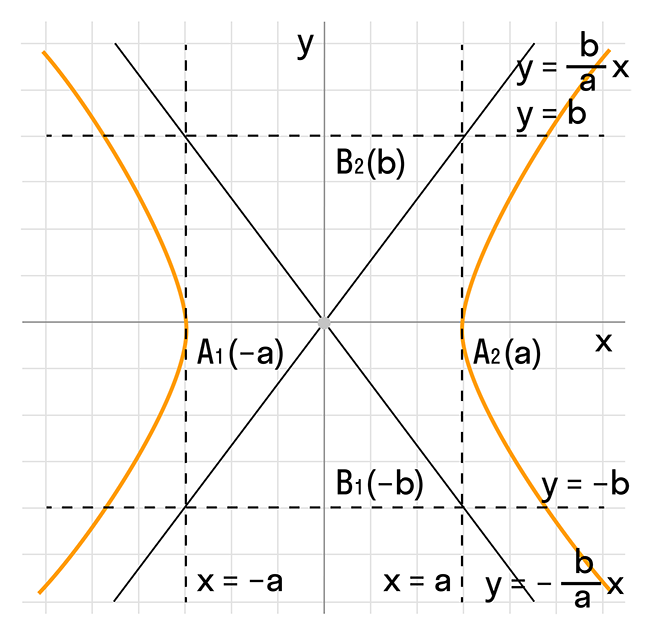
Гипербола имеет свои характерные особенности и форму, которые можно наблюдать в графическом представлении:
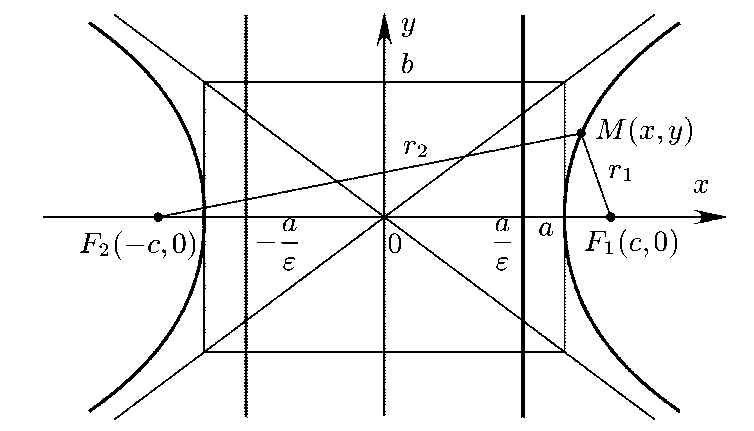
- Гипербола является симметричной относительно своего центра, который совпадает с серединой отрезка между фокусами.
- Действительная ось гиперболы - это отрезок, соединяющий вершины гиперболы, и имеет длину 2a, где a - действительная полуось гиперболы.
- Мнимая ось гиперболы - это прямая, которая перпендикулярна действительной оси и отложена от центра на расстояние b. Она имеет длину 2b.
- Расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию и обозначается как c.
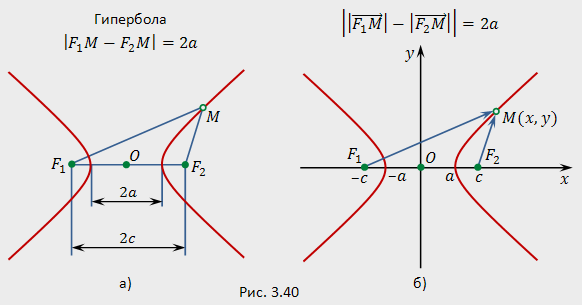
Пример построения гиперболы
Рассмотрим пример построения гиперболы по каноническому уравнению.
Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) - 4(y^2) = 20.
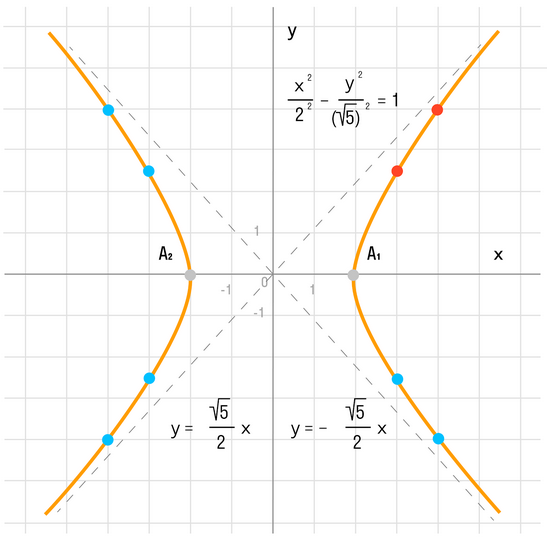
Решение: Для начала, уравнение можно привести к каноническому виду, разделив обе части на 20. Получим (x^2)/4 - (y^2)/5 = 1. Затем можем найти действительную и мнимую оси гиперболы, а также её вершины и фокусы.
Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 - 8(y^2)/20 = 1.
Решение: Здесь имеется иррациональный угловой коэффициент, но это не создает проблемы при построении гиперболы.
В результате, мы получаем графическое представление гиперболы с её оптическим свойством фокусировки световых лучей. Гипербола имеет важное значение в геометрии и оптике, и её свойства широко применяются в различных областях науки и техники.