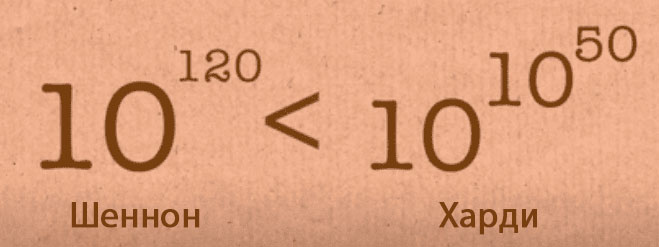Число Шеннона - это оценочное минимальное количество неповторяющихся шахматных партий, вычисленное в 1950 году американским математиком Клодом Шенноном. Узнайте, как было вычислено число Шеннона и сравните его с другими величинами. Познайте сложность и многообразие игры в шахматы.
Cодержание
Число́ Ше́ннона - это оценочное минимальное количество неповторяющихся шахматных партий, вычисленное в 1950 году американским математиком Клодом Шенноном. Оно составляет приблизительно 10120. Динамику роста этого числа можно проследить на примере обычной шахматной партии.

Вычисление числа Шеннона
Клод Шеннон описал вычисление числа Шеннона в своей работе "Программирование компьютера для игры в шахматы", опубликованной в марте 1950 года. В основу вычислений было положено предположение о том, что каждая игра длится в среднем 40 ходов, и на каждом ходу игрок делает выбор из среднего количества вариантов, равного 30.
Для первого хода у обеих сторон есть 40 различных вариантов. Для второго хода количество вариантов увеличивается до 676, а для третьего хода - до 576. Таким образом, на третьем ходу партии существует примерно 15,5 миллионов различных вариантов партии.
Если исключить откровенно глупые ходы, то это число можно сократить на 10-20%. Однако число Шеннона все равно остается огромным.

Сравнение с другими числами
Чтобы понять масштаб числа Шеннона, можно сравнить его с другими величинами. Количество атомов в наблюдаемой Вселенной составляет примерно 1079 до 1081, что в 1040 раз меньше числа Шеннона.
См. также
Количество возможных позиций
Кроме числа неповторяющихся партий, Шеннон также рассчитал количество возможных позиций, которое составляет приблизительно:
Это число, однако, включает также ситуации, исключаемые правилами игры и поэтому недосягаемые в дереве возможных ходов. В настоящее время появился ряд работ, уточняющих или даже опровергающих это число.
Заключение
Число Шеннона является оценочным минимальным количеством неповторяющихся шахматных партий. Оно демонстрирует огромную сложность и многообразие игры в шахматы. Даже при учете сокращения глупых ходов, число Шеннона остается колоссальным, превышающим количество атомов в наблюдаемой Вселенной.

Что нам скажет Википедия?
Число́ Ше́ннона — оценочное минимальное количество неповторяющихся шахматных партий, вычисленное в 1950 году американским математиком Клодом Шенноном. Составляет приблизительно 10120. Динамику роста этого числа можно проследить на примере обычной шахматной партии: для первого хода у обеих сторон есть 40 различных вариантов, для второго — ещё 676, для третьего — еще 576. Таким образом, всего на третьем ходу партии существует 40*676*576≈15,5 млн различных вариантов партии. Если исключить откровенно глупые ходы, то это число можно сократить на 10—20 %.
Вычисление числа Шеннона описано в работе «Программирование компьютера для игры в шахматы» (англ. «Programming a Computer for Playing Chess»), опубликованной в марте 1950 года в журнале Philosophical Magazine и ставшей одним из фундаментальных трудов в развитии компьютерных шахмат как дисциплины. В основу вычислений легло предположение о том, что каждая игра длится в среднем 40 ходов и на каждом ходе игрок делает выбор в среднем из 30 вариантов. Для сравнения — количество атомов в наблюдаемой Вселенной составляет по разным оценкам от 1079 до 1081, то есть в 1040 раз меньше числа Шеннона.
Кроме этого, Шеннон высчитал и количество возможных позиций, равняющееся примерно:
Это число, однако, включает также ситуации, исключаемые правилами игры и поэтому недосягаемые в дереве возможных ходов. В настоящее время появился ряд работ, уточняющих или даже опровергающих это число.