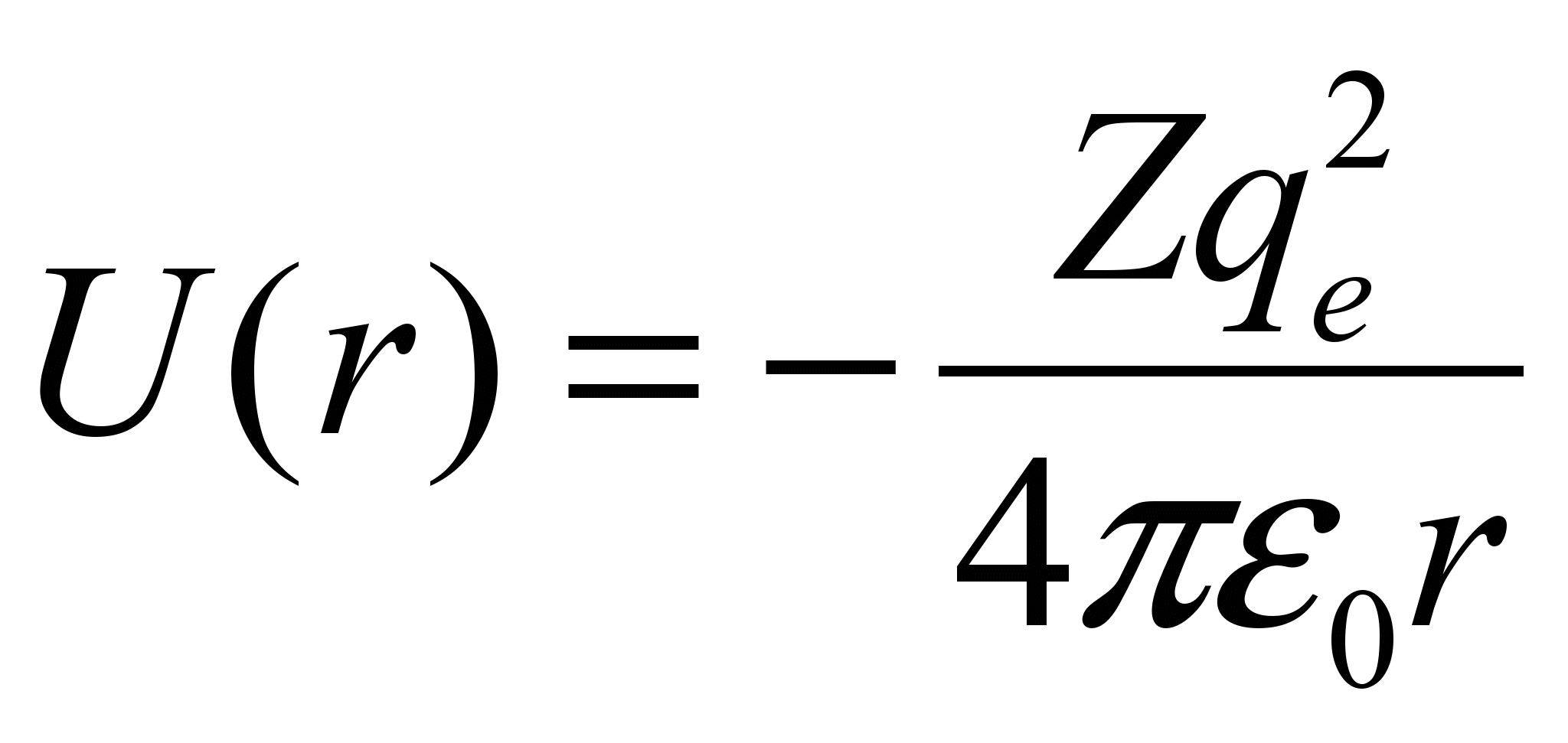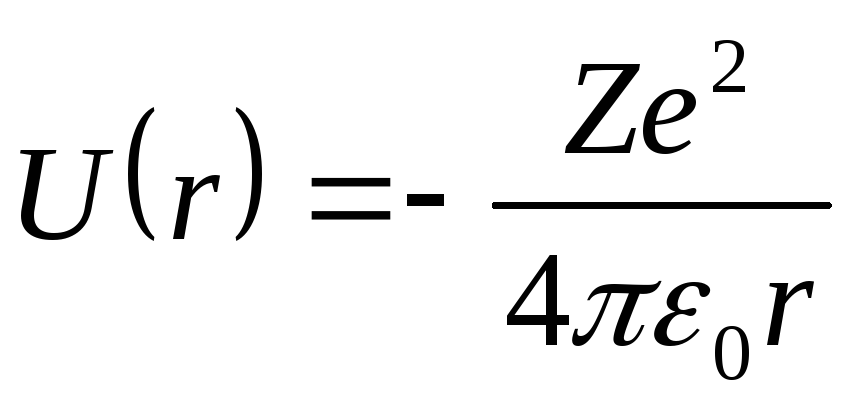Узнайте о связанной системе атома водорода, его энергетических состояниях и квантовых числах. Изучайте особенности атомной структуры и свойств химических элементов. Читайте статью на NOCFN.
Cодержание
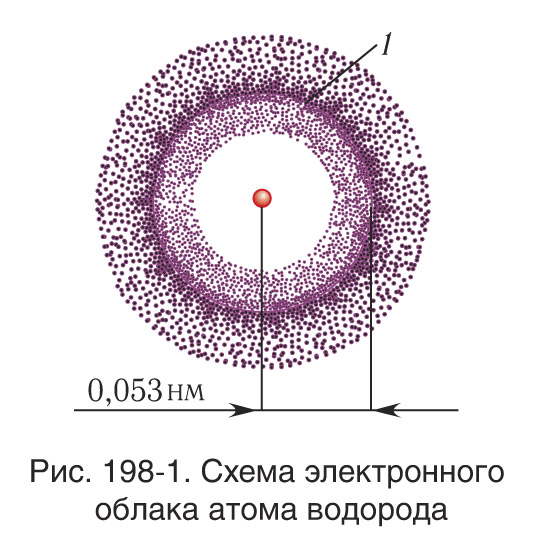
Атом водорода – связанная система, состоящая из положительно заряженного ядра – протона и отрицательно заряженного электрона. Размеры атома определяются размерами его электронной оболочки, которые составляют примерно 10-8 см.
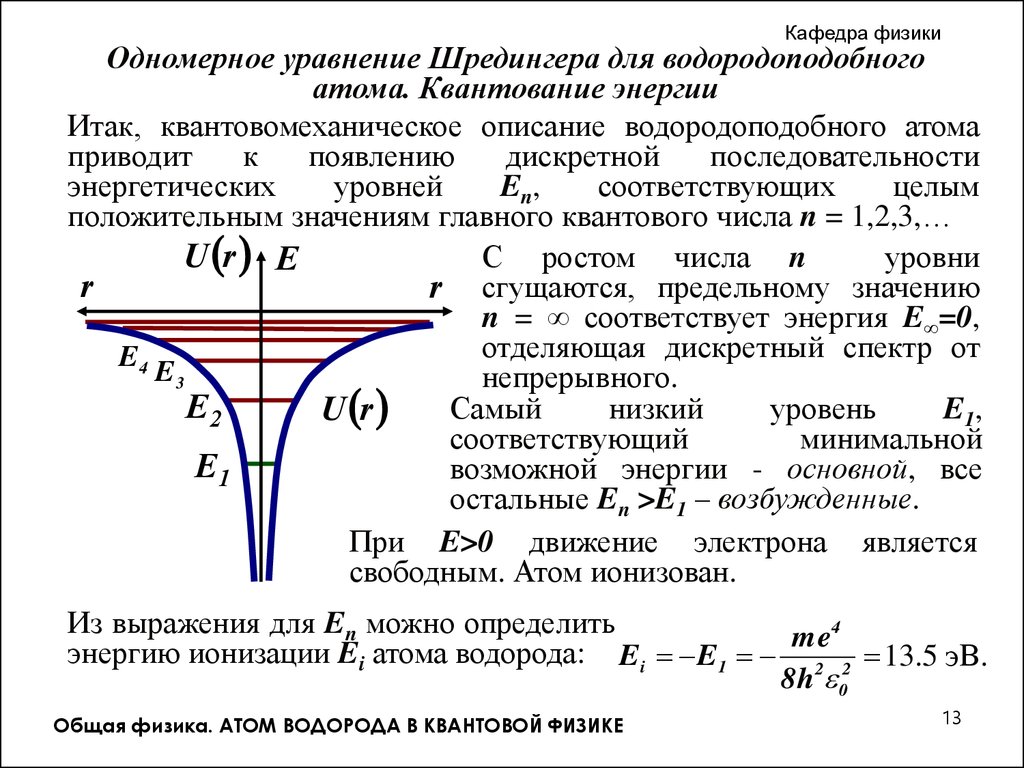
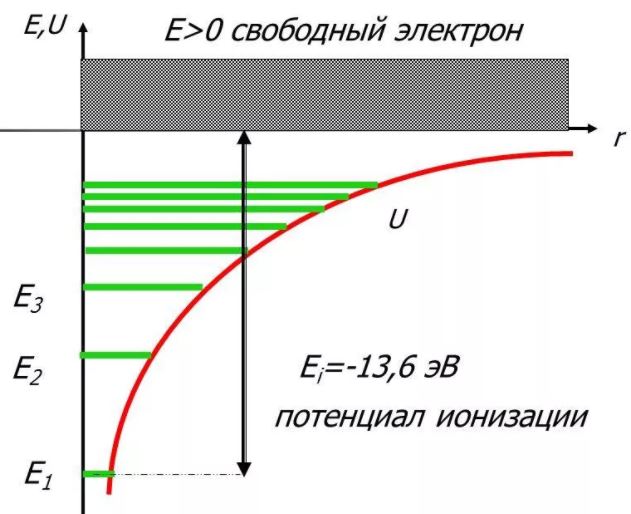
Энергии связанных состояний электрона в атоме водорода получаются при решении уравнения Шредингера с потенциалом V(r) = -e^2/r и определяются соотношением
E = -\frac{{Rhc}}{{n^2}}
где n – главное квантовое число, определяющее энергии различных состояний электрона в атоме водорода (n = 1, 2, 3...), R - постоянная Ридберга (R = 1.0974·10^5 см^-1).
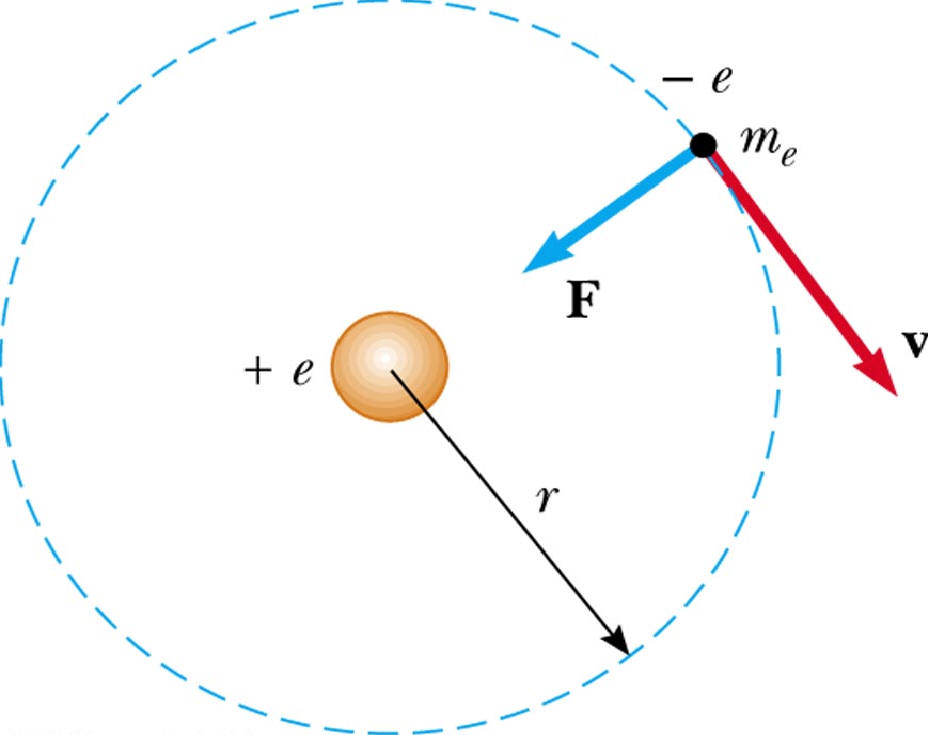
Уровни энергии и кратность вырождения
Каждому уровню с главным квантовым числом n соответствует n состояний, различающихся квантовыми числами l = 0, 1, 2, ..., (n-1). Такое вырождение уровней по энергии характерно только для кулоновского поля. Кроме того, каждое из этих вырожденных по l состояний (2l+1)-кратно вырождено по магнитному числу m = ±l, ±(l-1), ..., ±1, 0.
Таким образом, полная кратность вырождения стационарного квантового состояния с главным квантовым числом n дается соотношением
K = n^2
Такое рассмотрение справедливо при условии, что спин электрона равен нулю. Однако, так как электрон имеет спин s = 1/2, его полный момент количества движения J определяется векторной суммой его орбитального и спинового моментов:
J = L + S
Так как спин электрона s = 1/2, его полный момент количества движения J может быть только полуцелым.
При заданном значении орбитального момента l в атоме водорода возможно два состояния, различающихся значениями полного момента:
J = l + 1/2 и J = l - 1/2
Эти два значения различаются взаимными ориентациями орбитального и спинового векторов. Энергии электрона в состояниях l + 1/2 и l - 1/2 в кулоновском поле протона несколько отличаются, и вырождение по энергии состояний снимается. Это дополнительное взаимодействие носит название спин-орбитального. С учетом снятия вырождения спектр низколежащих состояний атома водорода обогащается, происходит тонкое расщепление уровней энергий.
Собственные функции и квантовые числа
Решение уравнения Шредингера для атома водорода позволяет найти собственные функции и определить квантовые числа, которые описывают состояния электрона.
Собственные функции уравнения Шредингера описывают стационарные состояния электрона и зависят от трех квантовых чисел: главного квантового числа n, орбитального квантового числа l и магнитного квантового числа m.
Главное квантовое число n определяет возможные значения энергии электрона в атоме водорода.
Орбитальное квантовое число l определяет модуль момента импульса электрона.
Магнитное квантовое число m определяет проекцию момента импульса электрона на заданное направление.
Количество состояний, соответствующих заданным значениям квантовых чисел, определяет кратность вырождения уровней энергии атома водорода.
См. также
Атом водорода в квантовой механике
Атом водорода в квантовой механике описывается двухчастичной матрицей плотности или волновой функцией. Волновая функция определяет вероятность обнаружить электрон в определенном месте пространства. Частичные решения уравнения Шредингера для атома водорода образуют счетное множество, и каждому состоянию присваивается уникальный трехзначный номер nlm.
Атом водорода имеет особое значение в квантовой механике, так как для него задача двух тел имеет точное или приближенное аналитическое решение. Результаты расчетов Бора, а также строгий квантовомеханический анализ, позволяют описать энергетические уровни атома водорода и форму атомных орбиталей.
В итоге, атом водорода является фундаментальной моделью в квантовой механике и играет важную роль в понимании атомной структуры и свойств других химических элементов.

Что нам скажет Википедия?
Атом водорода имеет особое значение в квантовой механике и релятивистской квантовой механике, поскольку для него задача двух тел имеет точное или приближённое аналитическое решение. Эти решения применимы для разных изотопов водорода (с соответствующими поправками).
В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощённо рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.
В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.
Результаты расчётов Бора были подтверждены в 1925—1926 годах строгим квантовомеханическим анализом, основанном на уравнении Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра выводится в аналитической форме. Оно описывает не только уровни энергии электрона и спектр излучения, но и форму атомных орбиталей.
Решение уравнения Шрёдингера для водородного атома использует тот факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следует полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента.